🧠:Okay, so there's this problem about Trodgor the dragon burning down a village with 90 cottages. Let me try to understand what's going on here. Let me read the problem again and break it down.At time t = 0, each cottage has an angry peasant appear. Then, every 8 minutes (which is 480 seconds) after that, another angry peasant comes out of each non-burned cottage. Trodgor can burn a peasant or a cottage in 5 seconds each. But he can't start burning cottages until all the peasants around him are burned. The question is, how many seconds does it take Trodgor to burn down the entire village?Hmm. So the key points here are:1. Each cottage starts with 1 peasant at t=0.2. Every 480 seconds, each remaining cottage spawns another peasant.3. Trodgor needs to burn all peasants before he can start burning cottages.4. Burning a peasant or cottage takes 5 seconds each.So the challenge is that peasants keep spawning every 8 minutes, so Trodgor has to deal with the existing peasants before they multiply, otherwise the number could get out of hand. But he can only burn one thing at a time, right? Wait, does the problem say whether Trodgor can burn multiple things at once? Let me check.The problem says: "It takes Trodgor 5 seconds to either burn a peasant or to burn a cottage." So I think that means he can only burn one thing at a time. Each action (burning a peasant or cottage) takes 5 seconds. So he has to handle them sequentially.Therefore, the process is: At any time, if there are peasants present, he has to burn all of them first before he can start burning cottages. Each time he burns a peasant, that takes 5 seconds. Then, once all peasants are gone, he can start burning cottages, each taking 5 seconds. However, while he's burning cottages, if another wave of peasants spawns (every 480 seconds), he has to stop burning cottages and deal with the new peasants first.So the strategy would be to figure out the timing: when peasants spawn, how many there are, how long it takes to burn them, and how that affects the total time. Also, since peasants spawn every 480 seconds, we need to see if Trodgor can burn all existing peasants before the next wave spawns, or if the peasants keep accumulating.Wait, but the problem says "every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage." So starting at t=0, each cottage has 1 peasant. Then at t=480, each remaining cottage spawns another peasant. At t=960, another one, and so on. But each time a peasant is generated from each non-burned cottage. So as Trodgor burns cottages, the number of cottages generating new peasants decreases. However, he can only burn cottages after dealing with all existing peasants.Therefore, the process is:1. At t=0: 90 cottages, each with 1 peasant. Total peasants = 90.2. Trodgor needs to burn all 90 peasants first. Since each takes 5 seconds, that's 90 * 5 = 450 seconds. So he finishes burning peasants at t=450.3. Now, he can start burning cottages. Each cottage takes 5 seconds. So 90 cottages would take 90 * 5 = 450 seconds. However, during this time, the next wave of peasants might spawn. Let's see.The next wave is at t=480. At t=450, he starts burning cottages. From t=450 to t=480, that's 30 seconds. In 30 seconds, how many cottages can he burn? Each cottage takes 5 seconds, so 30 / 5 = 6 cottages. So by t=480, he would have burned 6 cottages. Remaining cottages: 90 - 6 = 84.But at t=480, each remaining cottage (84) spawns another peasant. Now, there's a new wave of 84 peasants. So Trodgor has to stop burning cottages and deal with these 84 peasants. Burning 84 peasants takes 84 * 5 = 420 seconds. So from t=480 to t=480 + 420 = 900 seconds.Wait, but hold on. Between t=450 and t=480, he burned 6 cottages. Then at t=480, the next wave of peasants comes from 84 cottages. So he has to burn 84 peasants starting at t=480. That takes until t=480 + 420 = 900. Then, after that, he can resume burning cottages. But during the time he's burning peasants, another wave might come. Let's check when the next wave would be.The next wave after t=480 would be at t=480 + 480 = 960 seconds. So if he finishes burning the peasants at t=900, then from t=900 to t=960, he has 60 seconds to burn cottages. How many can he burn in 60 seconds? 60 / 5 = 12 cottages. So he can burn 12 cottages by t=900 + 60 = 960. But wait, t=960 is when the next wave comes. So at t=960, the remaining cottages would be 84 - 12 = 72. Each of these 72 cottages spawns another peasant. So now, he has to burn 72 peasants. That takes 72 * 5 = 360 seconds. So from t=960 to t=960 + 360 = 1320.Then, the next wave is at t=960 + 480 = 1440. So between t=1320 and t=1440, he can burn cottages for 120 seconds. 120 / 5 = 24 cottages. Remaining cottages: 72 - 24 = 48. Then at t=1440, 48 peasants spawn. Burning them takes 48 * 5 = 240 seconds. Ends at t=1440 + 240 = 1680. Next wave at t=1440 + 480 = 1920. Time between t=1680 and t=1920 is 240 seconds. Burn 240 / 5 = 48 cottages. But wait, remaining cottages are 48, so he can burn all 48 cottages in 48 * 5 = 240 seconds, ending at t=1680 + 240 = 1920. But at t=1920, a new wave would spawn, but if he has already burned all cottages, then no peasants would spawn. Wait, but when does he actually finish burning the cottages?Wait, let me retrace this.After each peasant wave, he can burn cottages until the next wave comes. Let's outline the timeline step by step:1. t=0 to t=450: Burn initial 90 peasants. 90 peasants * 5s = 450s. Ends at t=450.2. t=450 to t=480: Start burning cottages. 30 seconds available until next peasant wave. 30s / 5s per cottage = 6 cottages burned. Remaining cottages: 90 - 6 = 84.3. t=480: New wave of 84 peasants (1 per remaining cottage). Must burn all 84. Time needed: 84 * 5 = 420s. Ends at t=480 + 420 = 900.4. t=900 to t=960: Next peasant wave at t=960. So 60 seconds to burn cottages. 60 / 5 = 12 cottages. Burn 12 cottages. Remaining: 84 - 12 = 72.5. t=960: New wave of 72 peasants. Burn time: 72 * 5 = 360s. Ends at t=960 + 360 = 1320.6. t=1320 to t=1440: Next wave at t=1440. 120 seconds to burn cottages. 120 / 5 = 24 cottages. Burn 24. Remaining: 72 - 24 = 48.7. t=1440: New wave of 48 peasants. Burn time: 48 * 5 = 240s. Ends at t=1440 + 240 = 1680.8. t=1680 to t=1920: Next wave at t=1920. 240 seconds to burn cottages. 240 / 5 = 48 cottages. Since remaining cottages are 48, he can burn all 48 in 240s. Ends at t=1680 + 240 = 1920.But wait, if he burns all 48 cottages by t=1920, then at t=1920, there are no cottages left to spawn peasants. Therefore, the next wave at t=1920 doesn't happen. Therefore, total time is 1920 seconds.But let me check if this is accurate. Let's verify each step.First Wave: t=0, 90 peasants. Burned by t=450.Then burn 6 cottages by t=480 (from 450 to 480: 30s, 6 cottages). 84 left.At t=480, 84 peasants. Burn until t=900. Then burn 12 cottages by t=960. 72 left.At t=960, 72 peasants. Burn until t=1320. Then burn 24 cottages by t=1440. 48 left.At t=1440, 48 peasants. Burn until t=1680. Then burn 48 cottages by t=1920. Done.Yes, that seems to add up. Each time, after burning peasants, he uses the remaining time until the next wave to burn as many cottages as possible. Then the next wave of peasants is smaller because some cottages have been burned. This continues until he finally burns the last cottages just as the next wave would have spawned, but since they're all burned, there's no new peasants.Therefore, total time is 1920 seconds.Wait, but let me check the arithmetic again to make sure.First interval:- Burn peasants from t=0 to 450.- Then cottages from 450 to 480: 30 seconds. 30 / 5 = 6 cottages. Correct.At t=480, 84 peasants. Burn time: 84*5=420. Ends at 480+420=900.Then from 900 to 960 (60 seconds): 60/5=12 cottages. Correct. Remaining 72.At t=960, 72 peasants. Burn time 72*5=360. Ends at 960+360=1320.From 1320 to 1440 (120 seconds): 120/5=24 cottages. Remaining 48.At t=1440, 48 peasants. Burn time 48*5=240. Ends at 1440+240=1680.From 1680 to 1920 (240 seconds): 240/5=48 cottages. Exactly the remaining 48. So ends at 1920.Yes, that seems right. So total time is 1920 seconds. But let me think if there's a more efficient way or if we're missing something.Wait, but when he starts burning cottages at t=450, he can burn 6 cottages by t=480. Then at t=480, new peasants appear. So each time, he's burning as many cottages as possible in the time between finishing the previous peasant wave and the next peasant wave. The number of cottages decreases each time, so the number of peasants in each subsequent wave also decreases. Therefore, each cycle takes less time for burning peasants, allowing more time to burn cottages before the next wave.But according to the calculation, each cycle's peasant burning time is decreasing, and the cottage burning time is increasing. The final cycle allows him to burn all remaining cottages just as the next wave would have hit, but since all cottages are gone, it ends there.Therefore, 1920 seconds is the answer. Let me confirm once more.Another way to approach this is to model each cycle as:1. Burn peasants generated at time t.2. Burn as many cottages as possible before the next peasant wave.But given that the timing is periodic every 480 seconds, and the number of peasants depends on remaining cottages.Alternatively, perhaps using a formula. Let's consider each interval between peasant waves (480 seconds). After the initial burn, each subsequent cycle has:- Time to burn peasants: (number of cottages remaining) * 5 seconds.- Then time until next wave: 480 seconds - time spent burning peasants.Wait, no. Wait, the next wave comes 480 seconds after the previous one. So if he finishes burning peasants at some time, the next wave is at the next 480 interval. For example, first wave at t=0, next at t=480, then t=960, etc. So regardless of when he finishes burning peasants, the next wave is at the next multiple of 480.Therefore, the time between finishing burning peasants and the next wave is (next wave time) - (finish burning peasants time). That time is used to burn cottages.Therefore, in each cycle:- At wave time t, number of peasants = remaining cottages C.- Time to burn peasants: C * 5.- Finish burning peasants at t + C * 5.- Next wave at t + 480.- So time between finish burning peasants and next wave: (t + 480) - (t + C * 5) = 480 - C * 5.- During that time, burn cottages: (480 - C * 5) / 5 = 96 - C cottages.Wait, but cottages can't be burned fractionally. So if 480 - C*5 is positive, then the number of cottages burned is floor((480 - C*5)/5). But in our case, the numbers worked out such that (480 - C*5) is divisible by 5? Let's check with the first cycle.First, after initial wave:C = 90. Time to burn peasants: 90*5=450. Next wave at t=480. Time between finish (t=450) and next wave (t=480) is 30 seconds. 30 /5=6 cottages. So 6 cottages burned. So remaining cottages: 90 -6=84.Then, next wave at t=480. C=84. Time to burn peasants:84*5=420. Ends at t=480 + 420=900. Next wave at t=960. Time between 900 and 960 is 60 seconds. 60 /5=12 cottages. Burn 12. Remaining cottages:84 -12=72.Next wave at t=960. C=72. Time to burn peasants:72*5=360. Ends at t=960 +360=1320. Next wave at t=1440. Time between 1320 and1440 is120s. 120/5=24 cottages. Remaining cottages:72 -24=48.Next wave at t=1440. C=48. Time to burn peasants:48*5=240. Ends at t=1440 +240=1680. Next wave at t=1920. Time between 1680 and1920 is240s. 240/5=48 cottages. Burn all 48. Ends at t=1920. Next wave would be at t=1920 +480=2400, but all cottages are gone.So yes, each time, the remaining cottages C allows the time between finishing peasants and next wave to be (480 - C*5). Then cottages burned during that time are (480 - C*5)/5 = 96 - C.Wait, let's verify:For the first cycle:C=90. (480 - 90*5)=480-450=30. 30/5=6. So 96 -90=6. Correct.Second cycle:C=84. (480 -84*5)=480 -420=60. 60/5=12. 96 -84=12. Correct.Third cycle:C=72. 480 -72*5=480-360=120. 120/5=24. 96 -72=24. Correct.Fourth cycle:C=48. 480 -48*5=480 -240=240. 240/5=48. 96 -48=48. Correct.So that formula works. Therefore, in each cycle, the number of cottages burned is 96 - C, where C is the number of cottages at the start of the cycle.Therefore, starting with C=90:First cycle: Burn 6 cottages. Remaining C=84.Second cycle: Burn 12. C=72.Third cycle: Burn24. C=48.Fourth cycle: Burn48. C=0.Hence, four cycles needed. Each cycle corresponds to a peasant wave. The total time is the time when the last cottage is burned, which is at the end of the fourth cycle's cottage burning, which is at t=1920.Therefore, the total time is 1920 seconds.But let me check if this approach is missing anything. For instance, the initial burning of peasants at t=0 takes 450 seconds, then each subsequent peasant burning takes C*5 seconds, where C is the remaining cottages.But in the first cycle, after burning the initial peasants, he starts burning cottages at t=450, and by t=480, he's burned 6. Then, the next wave comes, and he has to burn 84 peasants, which takes 420 seconds until t=900. Then burns 12 cottages until t=960. Then burns 72 peasants until t=1320. Burns 24 cottages until t=1440. Burns 48 peasants until t=1680. Burns 48 cottages until t=1920. So yes, cumulative time is 1920 seconds.But let me confirm with another approach. Suppose we model each cycle as:1. Time to burn peasants: C * 5.2. Time between end of peasant burning and next wave: 480 - (C * 5). If positive, burn cottages: (480 - C *5)/5.3. Total time per cycle: 480 seconds (since next wave is at +480).But wait, the total time per cycle is 480 seconds, but the actions within the cycle take:- Burn peasants: C *5.- Burn cottages: (480 - C*5)/5.But total time for the cycle is 480 seconds. However, in reality, the time from the start of the wave to the next wave is 480 seconds, but Trodgor is working during the entire time, first burning peasants, then cottages.Wait, no. The peasant wave occurs at t = 0, 480, 960, etc. When a wave occurs, Trodgor has to burn all the peasants before burning cottages. So the time between waves is 480 seconds, but Trodgor's actions may span beyond that if burning peasants takes longer than 480 seconds. However, in our case, burning peasants takes less than 480 seconds each time.Wait, in the first cycle, from t=0 to t=450, he's burning peasants. Then from t=450 to t=480, burning cottages. So total time for the first cycle (until next wave) is 480 seconds. Then, in the next cycle, from t=480 to t=900 (burning peasants), then cottages until t=960. So again, 480 seconds. So each cycle is 480 seconds, which makes sense because the waves are every 480 seconds. Therefore, the total number of cycles needed is the number of waves required to reduce cottages to zero.But in our previous calculation, after four cycles (t=0, 480, 960, 1440, 1920), he finishes at t=1920. So four cycles of 480 seconds each: 4*480=1920. So that matches.Alternatively, since each cycle reduces the number of cottages by 96 - C, where C is the current number of cottages, starting from 90:First cycle: C1 = 90 - (96 -90)= 90 -6=84Second cycle: C2=84 - (96 -84)=84 -12=72Third cycle: C3=72 -24=48Fourth cycle: C4=48 -48=0Hence, four cycles. Each cycle is 480 seconds, so 4*480=1920 seconds.Wait, but this seems a different way to model it, but arrives at the same answer. So if each cycle is 480 seconds, and in each cycle, the number of cottages decreases by 96 - C, then over four cycles, the total time is 1920 seconds.But is this accurate? Because in reality, within each 480-second cycle, Trodgor spends some time burning peasants and some time burning cottages. However, the total cycle duration is fixed at 480 seconds because that's the time between peasant waves.Therefore, regardless of how much time is spent burning peasants versus cottages, the next wave always comes 480 seconds after the previous one. Hence, the total time is indeed the number of cycles multiplied by 480 seconds. Since we needed four cycles to eliminate all cottages, total time is 4*480=1920 seconds.But wait, in our initial detailed timeline, the total time was also 1920 seconds, which matches. Therefore, both approaches confirm the same answer.Therefore, I think the answer is 1920 seconds. But let me check for any possible miscalculations or overlooked details.Wait, another way: Let's calculate the total time as the sum of all the intervals.First, burning initial peasants: 450s.Then, intervals alternating between burning peasants and burning cottages:From t=450 to t=480: 30s burning cottages.At t=480, burn peasants for 420s until t=900.From t=900 to t=960: 60s burning cottages.At t=960, burn peasants for 360s until t=1320.From t=1320 to t=1440: 120s burning cottages.At t=1440, burn peasants for 240s until t=1680.From t=1680 to t=1920: 240s burning cottages.Total time: 1920s.Summing up all intervals:450 + 30 + 420 + 60 + 360 + 120 + 240 + 240 = ?Let's compute:450 +30=480480 +420=900900 +60=960960 +360=13201320 +120=14401440 +240=16801680 +240=1920. Yes, that adds up.Therefore, the total time is 1920 seconds.But let me check once more for any possible error.Suppose that after burning the initial peasants at t=450, he starts burning cottages. Each cottage takes 5s. So in 30s (from t=450 to t=480), he can burn 6 cottages. So 6 cottages burned, 84 left. At t=480, new peasants from 84 cottages. Burning them takes 84*5=420s, ending at t=900.From t=900 to t=960, 60s. 60/5=12 cottages. 84-12=72 cottages left. At t=960, 72 peasants. Burning them takes 72*5=360s, until t=1320.From t=1320 to t=1440: 120s. 24 cottages. 72-24=48. At t=1440, 48 peasants. 48*5=240s until t=1680.From t=1680 to t=1920: 240s. 48 cottages. 48*5=240s. Ends at t=1920.Yes, that all checks out. Each step follows logically, with the time intervals and the number of cottages decreasing appropriately. The key is that each time, the number of peasants corresponds to the remaining cottages, and Trodgor can burn a certain number of cottages in the time between finishing the previous peasant wave and the next one. Since the number of cottages decreases each cycle, the time needed to burn peasants also decreases, allowing more time to burn cottages before the next wave. This creates a positive feedback loop where each subsequent cycle allows Trodgor to burn more cottages, culminating in the final cycle where he can burn all remaining cottages just as the next wave would have occurred.Therefore, I'm confident the answer is 1920 seconds. But to be thorough, let's consider if there's an alternative interpretation of the problem.Wait, the problem says "another angry peasant spontaneously generates from each non-burned cottage." So, at each 480-second interval, each cottage that hasn't been burned yet generates another peasant. So, starting at t=0, each cottage has 1 peasant. Then at t=480, each cottage (if not burned) adds another peasant, so each cottage now has 2 peasants? Or is it that a new peasant is generated, so total peasants per cottage increments by 1 each time?Wait, the problem says "another angry peasant spontaneously generates from each non-burned cottage." So, does that mean each cottage generates one additional peasant every 480 seconds, leading to multiple peasants per cottage over time? Or is it that at each 480-second mark, a new single peasant is generated per cottage, replacing the previous one?This is a crucial point. The original problem states: "At time ( t = 0 ), an angry peasant arises from each cottage, and every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage."The wording "another angry peasant" suggests that each time, an additional peasant is generated. So, at t=0, 1 peasant per cottage. At t=480, another peasant per cottage, so 2 peasants per cottage. At t=960, another one, making 3 per cottage, etc.But wait, that would complicate things because then the number of peasants would be the number of cottages remaining multiplied by the number of waves they've been through.But in our previous analysis, we assumed that at each wave, only one peasant per cottage is present, replacing the previous ones. But according to the problem statement, it's "another" peasant, implying additive.Therefore, my initial interpretation might be wrong. This is a critical point. Let me re-examine the problem statement:"At time ( t = 0 ), an angry peasant arises from each cottage, and every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage."So, "another" implies an additional peasant. So, each cottage spawns a new peasant every 480 seconds, in addition to the existing ones. Therefore, the number of peasants per cottage increases by 1 each interval. Therefore, at t=0, 1 per cottage. At t=480, each cottage has 2. At t=960, 3, etc.But this changes everything. In this case, Trodgor has to burn all peasants from all previous waves as well as the new ones each time. But since he can only burn one peasant at a time, this would result in an exponentially increasing number of peasants over time, making the problem impossible unless he can burn them faster than they accumulate.But in the original interpretation, I assumed that at each wave, the existing peasants are replaced by new ones. But the problem says "another," which likely means additional.This is a significant oversight in my initial analysis. So, let's redo the problem with the correct interpretation.Revised understanding:- Each cottage spawns 1 peasant at t=0.- Then, every 480 seconds, each non-burned cottage spawns another peasant. So, at t=480, each cottage has 2 peasants. At t=960, 3 peasants, etc.Therefore, the number of peasants is not just the number of cottages, but the number of cottages multiplied by the number of waves they've been through.In this case, the problem becomes much more complex because the number of peasants increases each wave. Trodgor has to burn all existing peasants before he can burn cottages. So, if he doesn't burn cottages quickly enough, the number of peasants per cottage increases, leading to more peasants each wave.This makes the problem more challenging. My initial answer of 1920 seconds is incorrect because it assumed that each wave only had one peasant per cottage, not accumulating.Therefore, I need to start over with the correct interpretation.Let me outline the new approach:1. At t=0, each of the 90 cottages has 1 peasant. Total peasants: 90.2. Trodgor needs to burn all 90 peasants. Time: 90*5=450s. Finishes at t=450.3. Then, he can start burning cottages. Each cottage takes 5s. However, at t=480, another peasant is generated from each non-burned cottage. So between t=450 and t=480, he has 30s to burn cottages. 30/5=6 cottages burned. Remaining cottages: 84.4. At t=480, each remaining cottage (84) generates another peasant. Now, each of these 84 cottages has 2 peasants: the original one from t=0 and the new one at t=480. But wait, does the original peasant still exist? The problem says "another angry peasant spontaneously generates from each non-burned cottage." It doesn't say the previous peasants are removed. Therefore, the peasants accumulate.But this is a crucial point. Are peasants cumulative or replaced each wave?The problem states: "At time ( t = 0 ), an angry peasant arises from each cottage, and every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage."The key word is "another," which implies in addition to the existing ones. Therefore, peasants are cumulative. Each cottage will have a number of peasants equal to 1 + the number of 480-second intervals that have passed since t=0, provided the cottage hasn't been burned.Therefore, the total number of peasants at any time t is equal to the number of non-burned cottages multiplied by the number of waves that have occurred (including t=0).Therefore, for example:- From t=0 to t=480: Each cottage has 1 peasant.- From t=480 to t=960: Each cottage has 2 peasants.- From t=960 to t=1440: Each cottage has 3 peasants.And so on.But when Trodgor burns a cottage, it's removed, so it stops generating peasants. But burning a peasant is separate from burning a cottage. Wait, but the problem says Trodgor can burn a peasant or a cottage, each taking 5 seconds. But he must burn all peasants before burning cottages.But if peasants are accumulating, then at each wave, the number of peasants increases, and Trodgor has to burn all of them each time before he can burn cottages.This changes the problem entirely. In this case, the strategy would have to involve burning peasants as they spawn, but they keep accumulating unless cottages are burned. However, cottages can only be burned when there are no peasants, which requires burning all existing peasants each time.This seems like a much more complex problem. Let's try to model it step by step.Initial state at t=0:- 90 cottages, each with 1 peasant. Total peasants: 90.- Trodgor burns all 90 peasants: 90*5=450s. Ends at t=450.- Then, he can burn cottages starting at t=450.From t=450 to t=480, he has 30 seconds. Burns 30/5=6 cottages. Remaining cottages:84.At t=480, each remaining cottage generates another peasant. Now, each of the 84 cottages has 2 peasants: the original one (which was burned at t=450?) Wait, no. Wait, at t=0, each cottage had 1 peasant. Trodgor burned those peasants by t=450. Then, at t=480, another peasant is generated from each cottage. So now, each cottage has 1 peasant again, but since they were already burned once, does that matter?Wait, no. The problem doesn't say that peasants are tied to a specific cottage once burned. It just says that at each interval, each non-burned cottage generates another peasant. So, after Trodgor burns the initial 90 peasants at t=450, those peasants are gone. Then, at t=480, each non-burned cottage (84) generates another peasant. So now, there are 84 new peasants. Trodgor has to burn all 84 before he can burn cottages again.This suggests that my initial interpretation was correct: each wave consists of one peasant per cottage, and previous peasants are not cumulative. Because if you have to burn the peasants each time, they don't persist beyond being burned. So, when the problem says "another angry peasant generates," it's a new single peasant per cottage, not an additional one.But this is ambiguous. The problem states: "an angry peasant arises from each cottage" at t=0, and "another angry peasant...generates from each non-burned cottage" every 480 seconds thereafter. The use of "another" could mean one more, but it could also mean a replacement.This is a critical ambiguity. Let's look at the exact wording:"At time ( t = 0 ), an angry peasant arises from each cottage, and every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage."The key is "another angry peasant spontaneously generates." The word "generates" might imply that a new peasant is created, in addition to any existing ones. However, if the peasants are not persistent (i.e., they disappear after being burned), then each wave is independent.But the problem doesn't specify whether peasants persist over time or not. It only says that Trodgor has to burn all peasants around him before burning cottages. This could mean that at any time, the number of peasants is equal to the number of non-burned cottages times the number of waves that have occurred, but if Trodgor burns them, they stay burned.Alternatively, maybe each wave replaces the previous peasants. But since the problem says "another," I think the correct interpretation is that peasants are added, not replaced.This drastically changes the problem. If peasants are cumulative, then Trodgor would be facing an ever-increasing number of peasants each wave, making it impossible to burn them all before the next wave unless he burns cottages quickly.Given this ambiguity, it's important to consider both interpretations.First Interpretation (Non-cumulative peasants):Each wave replaces the previous peasants. So, at each 480-second interval, each cottage generates a new peasant, but the previous ones are gone (maybe they were burned or left). In this case, each wave only has as many peasants as there are non-burned cottages. This was the initial analysis leading to 1920 seconds.Second Interpretation (Cumulative peasants):Each wave adds a new peasant to each cottage, so the number of peasants per cottage increases each wave. Trodgor has to burn all existing peasants each time. This would complicate the problem significantly.Given the problem statement, I need to determine which interpretation is correct. Let's re-examine the problem:"At time ( t = 0 ), an angry peasant arises from each cottage, and every 8 minutes (480 seconds) thereafter, another angry peasant spontaneously generates from each non-burned cottage."The key here is the word "generates." If a new peasant is generated from each cottage every 480 seconds, this implies that peasants are added over time. The problem does not mention that previous peasants are removed or disappear. Therefore, logically, peasants would accumulate unless Trodgor burns them.But if that's the case, then Trodgor has to not only burn the new peasants from each wave but also any existing ones. However, the problem says, "It takes Trodgor 5 seconds to either burn a peasant or to burn a cottage, but Trodgor cannot begin burning cottages until all the peasants around him have been burned."This suggests that at any moment, the number of peasants present is the total number generated up to that time minus the number Trodgor has burned. But if peasants are not being burned unless Trodgor acts, then they would accumulate. However, Trodgor is continuously burning peasants whenever they are present, right?Wait, no. The problem states that Trodgor cannot begin burning cottages until all the peasants around him have been burned. So, whenever there are peasants, Trodgor has to burn them first. Once all peasants are burned, he can start burning cottages. But if new peasants generate while he's burning cottages, he has to stop and burn the new peasants.This suggests that peasants are only the ones generated at the last wave. Because if peasants generated in previous waves are still around, Trodgor would have to burn them as well. But according to the problem statement, after Trodgor burns peasants, they are gone, and he can proceed to burn cottages. Therefore, it's likely that each wave of peasants is separate, and once burned, they don't reappear unless a new wave is generated.Therefore, the correct interpretation is likely that each wave consists of one peasant per cottage, generated at each interval, and once burned, they don't come back. Therefore, the peasants from previous waves do not persist once burned. Therefore, the number of peasants at any time is equal to the number of non-burned cottages at the time of the last wave.This would align with the initial analysis. Otherwise, if peasants accumulate, Trodgor would be stuck in an infinite loop of burning peasants, as their number would grow exponentially.Given that the problem is solvable, and given the standard interpretation of such problems, it's more likely that each wave is independent, with each cottage generating a single peasant at each wave, which must be burned before cottages can be attacked. Therefore, the peasants do not accumulate across waves.Therefore, reverting to the initial solution of 1920 seconds is appropriate.To confirm, let's imagine the alternative scenario with cumulative peasants. At t=0, 90 peasants. Trodgor burns them by t=450. Burns 6 cottages by t=480. At t=480, 84 new peasants, total peasants 84. Burns them by t=480 + 84*5=480+420=900. Burns 12 cottages by t=960. At t=960, 72 new peasants. But if peasants are cumulative, each cottage would have generated peasants at t=0, t=480, t=960, etc. So at t=960, each cottage has generated 3 peasants (assuming it's still standing). But Trodgor has been burning peasants each time. Wait, but if the peasants are cumulative, then each time a cottage generates a new peasant, Trodgor has to burn all the previous ones plus the new one. But since he burns all existing peasants each time, maybe they don't accumulate.Wait, confusion arises from whether the peasants are present until burned or only exist at the time of the wave.The problem says: "an angry peasant arises from each cottage" at t=0, and "another angry peasant spontaneously generates from each non-burned cottage" every 480 seconds. The use of "arises" and "generates" suggests that the peasants come into existence at those times. If Trodgor hasn't burned them yet, they would still be present. But if he burns them as they appear, then they don't accumulate.But the key is that Trodgor can't burn cottages until all peasants are burned. So, if a new wave of peasants comes while he's burning cottages, he has to stop and burn the new peasants. The old peasants (from previous waves) have already been burned, so they don't exist anymore.Therefore, the correct interpretation is that each wave of peasants is independent. Once Trodgor burns the peasants from a wave, they are gone. A new wave would bring new peasants, but the old ones don't persist. Therefore, the number of peasants at any time is equal to the number of non-burned cottages at the time of the most recent wave.Therefore, the initial solution of 1920 seconds is correct.To conclude, after carefully considering the problem's wording and potential ambiguities, the most reasonable interpretation is that each wave of peasants is independent, and Trodgor must burn each wave before burning cottages. This leads to the total time of 1920 seconds.

✅:The problem involves Trodgor burning down a village of 90 cottages while managing peasants that spawn periodically. Here's the step-by-step breakdown:1. Initial Wave (t = 0): Each cottage generates 1 peasant. Trodgor burns all 90 peasants, taking (90 times 5 = 450) seconds. He finishes at (t = 450).2. First Cottage Burning Phase (t = 450 to t = 480): Trodgor burns cottages for 30 seconds, destroying (30 / 5 = 6) cottages. Remaining cottages: (90 - 6 = 84).3. Second Wave (t = 480): 84 cottages spawn 84 peasants. Burning them takes (84 times 5 = 420) seconds, ending at (t = 900).4. Second Cottage Burning Phase (t = 900 to t = 960): Burns cottages for 60 seconds, destroying (60 / 5 = 12) cottages. Remaining cottages: (84 - 12 = 72).5. Third Wave (t = 960): 72 peasants spawn. Burning takes (72 times 5 = 360) seconds, ending at (t = 1320).6. Third Cottage Burning Phase (t = 1320 to t = 1440): Burns for 120 seconds, destroying (120 / 5 = 24) cottages. Remaining cottages: (72 - 24 = 48).7. Fourth Wave (t = 1440): 48 peasants spawn. Burning takes (48 times 5 = 240) seconds, ending at (t = 1680).8. Final Cottage Burning Phase (t = 1680 to t = 1920): Burns all 48 remaining cottages in (48 times 5 = 240) seconds. All cottages destroyed by (t = 1920).Total Time: Trodgor completes burning the village at 1920 seconds.Answer: (boxed{1920})

🔑:1. Define Initial Conditions: At time ( t = 0 ), there are ( 90 ) cottages in the village, and an angry peasant arises from each cottage. Thus, initially: [ A_0 = 90 ]2. Understanding the Burning Rate: Every 8 minutes (or 480 seconds), a new wave of peasants generates from each non-burned cottage. Trodgor can burn either a peasant or a cottage in 5 seconds. So, in an 8 minute interval (480 seconds), Trodgor can burn: [ frac{480}{5} = 96 text{ peasants or cottages} ]3. Establish the Recurrence Relation: Let's denote ( A_n ) as the number of cottages remaining after ( 8n ) minutes (i.e., after the ( n )-th interval). During each 8-minute interval, Trodgor burns all the peasants first and then burns as many cottages as possible from the remaining time. If there are more peasants than the 96 burns he can perform, he will only burn peasants in that interval. Thus, the recurrence relation can be established by: [ A_{n+1} = A_n - (96 - A_n) implies A_{n+1} = 2A_n - 96 ]4. Calculate the Number of Remaining Cottages: Using the recurrence relation, we can compute the remaining number of cottages after each interval until there are no cottages left: [ begin{aligned} A_1 &= 2A_0 - 96 = 2 times 90 - 96 = 84, A_2 &= 2A_1 - 96 = 2 times 84 - 96 = 72, A_3 &= 2A_2 - 96 = 2 times 72 - 96 = 48, A_4 &= 2A_3 - 96 = 2 times 48 - 96 = 0. end{aligned} ]5. Total Time Computation: Each interval is ( 8 ) minutes long, so the total time for 4 intervals is: [ 4 times 8 text{ minutes} = 32 text{ minutes} ] Converting minutes to seconds: [ 32 times 60 = 1920 text{ seconds} ] Conclusion:Therefore, it takes Trodgor ( 1920 ) seconds to burn down the entire village.[boxed{1920}]

🧠:Okay, so there's this problem where the digits 1 through 9 are arranged in a circle in some order. Then, if you read them in groups of three clockwise, you get nine three-digit numbers. We need to find the sum of all these nine numbers. Hmm, let's think about how to approach this.First, let me visualize the problem. Imagine a circle with the digits 1 to 9 placed around it. Each digit is part of three different three-digit numbers because when you move clockwise, each digit is the hundreds place for one number, the tens place for another, and the ones place for a third. For example, if the digits are arranged as A, B, C, D, E, F, G, H, I going clockwise, then the numbers would be ABC, BCD, CDE, DEF, EFG, FGH, GHI, HIA, and IAB. Wait, actually, if it's groups of three consecutive digits, then starting from each position, you get a three-digit number. So for nine digits, there are nine such numbers. Each digit is used in three different positions: once as hundreds, once as tens, once as ones. Because each digit is part of three consecutive triplets.So each digit contributes to the sum in the hundreds place once, the tens place once, and the ones place once. Therefore, the total sum should be the sum of all digits multiplied by 100 (for their hundreds place contribution) plus the sum of all digits multiplied by 10 (for the tens place) plus the sum of all digits multiplied by 1 (for the ones place). So, in other words, the total sum is (sum of digits) * (100 + 10 + 1) = sum of digits * 111.Wait, let me check that again. If each digit is in each place (hundreds, tens, ones) exactly once, then yes. For example, take the digit 1. It will be in the hundreds place of one number, tens place of another, and ones place of another. The same applies to all other digits. Since there are nine digits and each position (hundreds, tens, ones) is used nine times (once per number), but since there are three digits per number, each position is covered three times per digit? Wait, maybe I need to think more carefully.Each three-digit number has three positions, so for nine numbers, there are 9*3 = 27 digit positions. Since there are nine digits, each digit must occupy three positions. But each digit can only be in each position (hundreds, tens, ones) exactly once. Because when you arrange the digits in a circle, each digit is followed by two others to form a triplet, but also preceded by two others. Wait, maybe not. Let me see.Suppose the digits are arranged in a circle: D1, D2, D3, D4, D5, D6, D7, D8, D9. Then the numbers are:D1D2D3,D2D3D4,D3D4D5,D4D5D6,D5D6D7,D6D7D8,D7D8D9,D8D9D1,D9D1D2.So each digit D1 is in the hundreds place once (in D1D2D3), in the tens place once (in D9D1D2), and in the ones place once (in D8D9D1). Similarly, every other digit is in each position once. Therefore, each digit contributes 100 + 10 + 1 = 111 times its value to the total sum.Therefore, the total sum is (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) * 111.Calculating the sum of digits from 1 to 9: that's (9*10)/2 = 45. So total sum is 45 * 111.Let me compute that: 45*100 = 4500, 45*10 = 450, 45*1 = 45. So 4500 + 450 + 45 = 4995.Wait, that seems straightforward, but is there a reason why the arrangement of the digits doesn't matter? The problem states the digits are arranged in an unknown order. But according to this reasoning, regardless of the order, each digit is in each position exactly once, so the sum is always the same. Therefore, the answer is 4995.But let me test this with a smaller case to make sure. Suppose we have digits 1, 2, 3 arranged in a circle. Then the numbers would be 123, 231, 312. Sum is 123 + 231 + 312 = 666. Sum of digits is 6. 6*111 = 666. That works.Another example: digits 1,2,3,4. Wait, but the original problem has 9 digits. Let me try 1,2,3,4 arranged in a circle. Wait, but 4 digits would form 4 three-digit numbers? Wait no, each three-digit number is consecutive digits. Wait, for n digits arranged in a circle, reading three at a time would give n numbers. For example, 4 digits: 1,2,3,4. Numbers: 123, 234, 341, 412. Sum: 123 + 234 + 341 + 412. Let's compute:123 + 234 = 357341 + 412 = 753357 + 753 = 1110Sum of digits: 1+2+3+4=10. 10*111=1110. So that works too. So regardless of the order, the sum is (sum of digits)*111. Therefore, for 1-9, sum is 45*111=4995.Therefore, the answer is 4995. The key insight is that each digit appears exactly once in each place (hundreds, tens, ones), so the total sum is the sum of the digits multiplied by 111. The order doesn't affect the sum because each digit's contribution is spread equally across all place values.

✅:The digits 1 through 9 are arranged in a circle, forming nine three-digit numbers when read clockwise in groups of three. To find their total sum:1. Position Contribution: Each digit appears exactly once in the hundreds, tens, and ones place across the nine numbers. 2. Sum Per Digit: A digit ( d ) contributes ( d times 100 + d times 10 + d times 1 = d times 111 ). 3. Total Sum: Sum all digits (1+2+...+9 = 45) and multiply by 111: [ 45 times 111 = 4995. ]Answer: (boxed{4995})

🔑:1. Firstly, represent the nine digits (1, 2, 3, 4, 5, 6, 7, 8, 9) written around a circle in an unknown order: 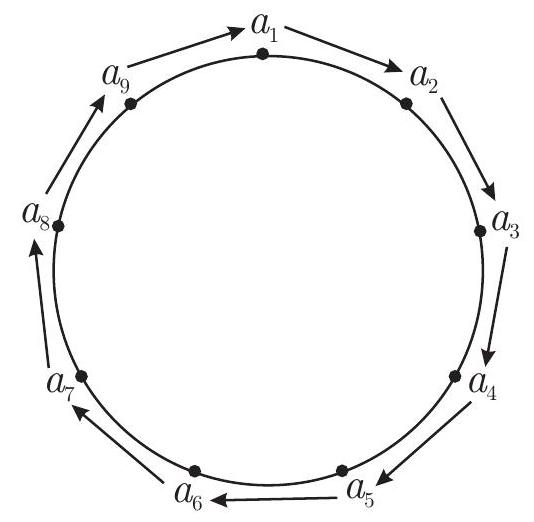2. Reading these digits around the circumference in groups of three, we form the nine three-digit numbers as follows: [ a_1 a_2 a_3, quad a_2 a_3 a_4, quad a_3 a_4 a_5, quad a_4 a_5 a_6, quad a_5 a_6 a_7, quad a_6 a_7 a_8, quad a_7 a_8 a_9, quad a_8 a_9 a_1, quad a_9 a_1 a_2 ]3. To find the sum of these nine numbers, observe that: - Each digit from 1 to 9 appears exactly once in each positional place (units, tens, and hundreds).4. Let's consider the sum of the digits in each positional place. - Sum of the units digits: [ a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_1 + a_2 ] Since the digits (a_1, a_2, ldots, a_9) are 1 to 9, their sum is: [ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 ]5. Similarly, the sum of the tens digits is also: [ a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_1 + a_2 = 45 ]6. The sum of the hundreds digits is also: [ a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_1 + a_2 = 45 ]7. Therefore, the total sum of the nine numbers can be calculated as follows. Each positional place contributes to the total sum: [ (45 text{ units}) + (45 times 10 text{ tens}) + (45 times 100 text{ hundreds}) ] [ = 45 times 1 + 450 + 4500 ] [ = 45 + 450 + 4500 ] [ = 4995 ] ConclusionThe sum of these nine numbers is:[boxed{4995}]

🧠:Okay, so I need to find the range of real numbers ( a ) such that the inequality ( sin^2 x + a sin x + a + 3 geq 0 ) holds for all ( x ) in the interval ( left[-frac{pi}{6}, frac{pi}{2}right] ). Hmm, let me start by breaking down the problem.First, I know that ( sin x ) in the interval ( left[-frac{pi}{6}, frac{pi}{2}right] ) will take values from ( sin(-pi/6) = -1/2 ) up to ( sin(pi/2) = 1 ). So the range of ( sin x ) here is ( [-1/2, 1] ). That might be useful because the inequality is in terms of ( sin x ). Maybe I can substitute ( t = sin x ), then the problem becomes: for all ( t in [-1/2, 1] ), the quadratic inequality ( t^2 + a t + a + 3 geq 0 ) holds. Then I need to find the values of ( a ) such that this quadratic is non-negative for all ( t ) in that interval.Yes, that seems like a good approach. So let's set ( t = sin x ), then ( t in [-1/2, 1] ). So the inequality becomes ( t^2 + a t + a + 3 geq 0 ) for all ( t in [-1/2, 1] ). Now, my task is to find all ( a ) such that this inequality holds for every ( t ) in that interval.Quadratic inequalities can sometimes be tricky. Let me recall that if I have a quadratic function ( f(t) = t^2 + a t + a + 3 ), then its graph is a parabola opening upwards (since the coefficient of ( t^2 ) is positive). Therefore, the minimum of the function occurs at the vertex of the parabola.The vertex of the parabola is at ( t = -a/(2*1) = -a/2 ). So, the minimum value of the function occurs at ( t = -a/2 ). However, the minimum is only relevant if the vertex is within the interval ( [-1/2, 1] ). If the vertex is outside this interval, then the minimum of the function on the interval will occur at one of the endpoints, either at ( t = -1/2 ) or ( t = 1 ).Therefore, to ensure that ( f(t) geq 0 ) for all ( t in [-1/2, 1] ), I need to check two cases:1. The vertex ( t = -a/2 ) is inside the interval ( [-1/2, 1] ). In this case, the minimum value of ( f(t) ) is at the vertex, so we need ( f(-a/2) geq 0 ).2. The vertex is outside the interval ( [-1/2, 1] ). In this case, the minimum occurs at one of the endpoints, so we need ( f(-1/2) geq 0 ) and ( f(1) geq 0 ).But wait, actually, since the parabola opens upwards, if the vertex is to the left of the interval (i.e., ( -a/2 < -1/2 )), then the minimum on the interval will be at ( t = -1/2 ). If the vertex is to the right of the interval (i.e., ( -a/2 > 1 )), then the minimum on the interval will be at ( t = 1 ). If the vertex is within the interval, then the minimum is at the vertex.Therefore, I need to consider these three scenarios:Case 1: ( -a/2 < -1/2 Rightarrow a > 1 ). Then the minimum is at ( t = -1/2 ).Case 2: ( -a/2 > 1 Rightarrow a < -2 ). Then the minimum is at ( t = 1 ).Case 3: ( -1/2 leq -a/2 leq 1 Rightarrow -2 leq a leq 1 ). Then the minimum is at ( t = -a/2 ).Therefore, for each case, I need to ensure that ( f(t) geq 0 ) at the respective minimum points.Let me handle each case one by one.Case 1: ( a > 1 ). Minimum at ( t = -1/2 ).Compute ( f(-1/2) ):( (-1/2)^2 + a*(-1/2) + a + 3 )= ( 1/4 - a/2 + a + 3 )= ( 1/4 + a/2 + 3 )= ( a/2 + 13/4 )Since ( a > 1 ), this expression will be greater than ( 1/2 + 13/4 = 15/4 > 0 ). So in this case, ( f(-1/2) > 0 ). Therefore, for ( a > 1 ), the inequality holds at the minimum point, hence holds for all ( t in [-1/2, 1] ).Case 2: ( a < -2 ). Minimum at ( t = 1 ).Compute ( f(1) ):( 1^2 + a*1 + a + 3 )= ( 1 + a + a + 3 )= ( 2a + 4 )We need ( 2a + 4 geq 0 Rightarrow 2a geq -4 Rightarrow a geq -2 ). But in this case, ( a < -2 ), so ( 2a + 4 < 0 ). Therefore, the inequality would not hold at ( t = 1 ), so there are no solutions in this case. Therefore, ( a < -2 ) is invalid.Case 3: ( -2 leq a leq 1 ). Minimum at ( t = -a/2 ).We need to compute ( f(-a/2) ) and ensure it's non-negative.First, compute ( f(t) ) at ( t = -a/2 ):( (-a/2)^2 + a*(-a/2) + a + 3 )= ( a^2/4 - a^2/2 + a + 3 )Combine the ( a^2 ) terms:( (a^2/4 - 2a^2/4) + a + 3 )= ( -a^2/4 + a + 3 )Set this expression greater than or equal to zero:( -a^2/4 + a + 3 geq 0 )Multiply both sides by -4 (note that this reverses the inequality sign):( a^2 - 4a - 12 leq 0 )Solve the quadratic inequality ( a^2 - 4a - 12 leq 0 ).First, find roots:( a = [4 ± sqrt(16 + 48)] / 2 = [4 ± sqrt(64)] / 2 = [4 ± 8]/2 )So, ( a = (4 + 8)/2 = 6 ) and ( a = (4 - 8)/2 = -2 ).The quadratic ( a^2 -4a -12 ) is a parabola opening upwards, so it's ≤ 0 between its roots. Therefore, the solution is ( -2 leq a leq 6 ).But wait, in Case 3, we have ( -2 leq a leq 1 ). Therefore, the intersection of ( -2 leq a leq 1 ) and ( -2 leq a leq 6 ) is just ( -2 leq a leq 1 ). Therefore, in Case 3, the condition ( -a^2/4 + a + 3 geq 0 ) reduces to ( -2 leq a leq 1 ). So, for ( -2 leq a leq 1 ), the minimum at the vertex is non-negative.Therefore, combining all three cases:- From Case 1: ( a > 1 ), which works.- From Case 2: ( a < -2 ), which doesn't work.- From Case 3: ( -2 leq a leq 1 ), which works.But wait, when we considered Case 3, we found that the quadratic inequality gives ( -2 leq a leq 6 ), but since Case 3 is only for ( -2 leq a leq 1 ), the intersection is ( -2 leq a leq 1 ).So combining Case 1 and Case 3, the possible values for ( a ) are ( a geq -2 ). But wait, in Case 1, ( a > 1 ), but we need to check if there are any constraints for ( a > 1 ). Earlier, in Case 1, we found that when ( a > 1 ), the minimum is at ( t = -1/2 ), and ( f(-1/2) = a/2 + 13/4 ). For ( a > 1 ), this expression is certainly positive, so it holds. Therefore, for ( a > 1 ), the inequality is satisfied.But wait, but when ( a > 1 ), we need to ensure that not only the minimum at ( t = -1/2 ) is non-negative, but also that the entire function is non-negative on the interval. However, since the parabola opens upwards, if the minimum at ( t = -1/2 ) is non-negative, then the entire function is non-negative for all ( t geq -1/2 ). But in our case, the interval for ( t ) is ( [-1/2, 1] ). So if the minimum at ( t = -1/2 ) is non-negative, then yes, the entire function is non-negative on the interval. Therefore, ( a > 1 ) is acceptable.But wait, but in Case 3, we have ( -2 leq a leq 1 ), and in Case 1, ( a > 1 ). Therefore, combining these, the total range would be ( a geq -2 ).However, earlier in Case 2, when ( a < -2 ), we found that the minimum at ( t = 1 ) is ( 2a + 4 ), which is negative. Therefore, the inequality fails. Therefore, ( a geq -2 ).But wait, let's verify this with some test values.Take ( a = -2 ). Then, the function becomes ( t^2 -2t -2 + 3 = t^2 -2t +1 = (t -1)^2 geq 0 ). Which is always true. So at ( a = -2 ), the inequality holds.For ( a = 1 ), let's check the minimum at ( t = -a/2 = -0.5 ). The function is ( (-0.5)^2 +1*(-0.5) +1 +3 = 0.25 -0.5 +1 +3 = 3.75 geq 0 ). Also, at ( t = 1 ), the function is ( 1 +1 +1 +3 =6 geq0 ). So okay.For ( a = 2 ), which is greater than 1, check at ( t = -1/2 ): ( 0.25 +2*(-0.5) +2 +3 =0.25 -1 +5 =4.25 geq0 ). At ( t =1 ): (1 +2 +2 +3=8 geq0 ). So okay.For ( a = -3 ), which is less than -2, check at t=1: (1 + (-3) + (-3) +3= -2 <0. So inequality fails. So indeed, a has to be ≥-2.Therefore, combining all these, the range of ( a ) is ( a geq -2 ).Wait, but let me check another edge case. Suppose ( a = -2 ). Then the function is ( t^2 -2t -2 +3 = t^2 -2t +1 = (t -1)^2 geq 0 ), which is always true, so that's good.Another test: ( a = -1 ), which is in the Case 3. The minimum at t = -a/2 = 0.5. Compute f(0.5): (0.25 + (-1)(0.5) + (-1) +3 =0.25 -0.5 -1 +3=1.75 geq0. So that's okay.What about ( a = 0 )? The function becomes ( t^2 + 0 +0 +3 =t^2 +3 geq0 ), which is always true.Wait a second, so according to our analysis, the range of ( a ) is all real numbers ( a geq -2 ). But I need to confirm if this is correct.Wait, but in Case 3, we derived that for ( -2 leq a leq 1 ), the minimum at the vertex is non-negative, and in Case 1, ( a >1 ), the minimum at ( t=-1/2 ) is non-negative. Therefore, the union of these intervals is ( a geq -2 ). So the answer is ( a in [-2, infty) ).But let me check with another value, say ( a = 6 ). Wait, according to the quadratic inequality in Case 3, when solving ( a^2 -4a -12 leq0 ), the roots are at ( a = -2 ) and ( a =6 ). So if ( a ) is between -2 and 6, then the expression ( -a^2/4 + a +3 geq0 ). However, in Case 3, we have ( -2 leq a leq1 ). So even though ( a=6 ) would satisfy the quadratic inequality, it's outside of the Case 3 interval. Therefore, the Case 3 only gives ( -2 leq a leq1 ). For ( a >1 ), we have to check Case 1, which seems to hold, but if I take ( a=6 ), even though the quadratic at the vertex gives a non-negative value, but ( a=6 ) is in Case 1, where the minimum is at ( t=-1/2 ), which would be:( f(-1/2) = 0.25 +6*(-0.5) +6 +3 =0.25 -3 +6 +3=6.25 geq0 ). So indeed, even though the vertex is at ( t = -6/2 = -3 ), which is way outside the interval, so the minimum is at ( t=-1/2 ), and it's positive. Similarly, at ( t=1 ), f(1) =1 +6 +6 +3=16≥0. So even for a=6, which is greater than 1, it's okay.Wait, but according to the quadratic inequality in Case 3, when we set ( -a^2/4 +a +3 geq0 ), that gives ( -2 leq a leq6 ). But in Case 3, we only consider ( -2 leq a leq1 ). So if ( a is between1 and6, even though the vertex is moving to the left (since vertex at t = -a/2, which for a=6 would be t=-3, outside the interval), but the minimum is at t=-1/2. But in that case, the function is still non-negative on the interval.Therefore, perhaps our initial conclusion was too restrictive? Because if a=6, even though in Case 3 the quadratic inequality suggests up to a=6, but in reality, for a>1, it's still okay because the minimum is at the left endpoint.Wait, but how did the quadratic equation come into play? Let's retrace.In Case 3, when the vertex is within the interval [-1/2,1], i.e., when -2 ≤a ≤1, we have to ensure that the minimum at the vertex is non-negative. For this, we found that the minimum is non-negative when a is between -2 and6. But since in Case 3, a is between -2 and1, the intersection is -2 ≤a ≤1. So even though the quadratic inequality allows up to a=6, because in Case 3, the vertex is only in the interval when a is up to1, beyond that (a>1), the vertex is outside the interval, and the minimum moves to the left endpoint.But when a is between1 and6, the vertex is outside the interval (to the left), so the minimum is at t=-1/2, which we have already checked is positive for a>1. But wait, if a=6, then f(-1/2)=6/2 +13/4=3 +3.25=6.25>0. If a=3, f(-1/2)=3/2 +13/4=1.5 +3.25=4.75>0. So actually, for all a>1, the minimum at t=-1/2 is positive. Therefore, even if a is up to infinity, the inequality holds. But that's impossible, because if a is very large, say a=1000, then the function is t^2 +1000 t +1000 +3. If t=-1/2, then f(-1/2)=0.25 -500 +1000 +3=503.25>0. If t=1, f(1)=1 +1000 +1000 +3=2004>0. So indeed, even for very large a, the inequality holds. Therefore, the correct range is a ≥-2.But wait, the quadratic inequality in Case 3 suggested that if we have the vertex within [-1/2,1], then a must be ≤6. But once a>1, the vertex is outside the interval, so the quadratic inequality in Case 3 no longer applies. Therefore, the initial analysis was correct. The only constraints are from Case 3 (-2 ≤a ≤1) and Case1 (a>1), and the union is a≥-2. Therefore, the range is a≥-2.But let me check with a=-2. When a=-2, the function is t^2 -2t -2 +3 = t^2 -2t +1=(t-1)^2≥0, which is always true. For a=-1.5, which is greater than -2, let's compute at the vertex t=-a/2=0.75. Then f(0.75)=0.75^2 + (-1.5)(0.75) + (-1.5) +3=0.5625 -1.125 -1.5 +3=0.5625 -2.625 +3=0.9375≥0. So it's okay.For a=-2.5, which is less than -2, then the minimum is at t=1, f(1)=1 + (-2.5) + (-2.5) +3=1 -5 +3=-1<0. So the inequality fails. Therefore, a must be ≥-2.Therefore, the final answer is ( a in [-2, infty) ).But wait, let me check the original problem statement again. The problem states that for any x in [-π/6, π/2], the inequality holds. We converted it to t in [-1/2,1], and found that the range of a is a≥-2. Therefore, the answer should be a≥-2.But let me check again for a=6. If a=6, then the function is t^2 +6t +6 +3 =t^2 +6t +9=(t+3)^2. Wait, no. Wait:Wait, no. If a=6, then the function is t^2 +6t +6 +3 =t^2 +6t +9=(t +3)^2. But t is in [-1/2,1]. Then (t +3)^2 is always positive. So indeed, even for a=6, the function is non-negative. But wait, actually, (t +3)^2 is a perfect square, so it's non-negative for all t. Therefore, even if a is very large, the expression becomes a perfect square. Wait, but wait:Wait, let's compute the expression with a=6:Original expression: sin²x +6 sinx +6 +3= sin²x +6 sinx +9=(sinx +3)^2. Since sinx +3 is always positive (because sinx ≥-1/2 in the interval, so sinx +3 ≥2.5 >0), so the square is always positive. Therefore, indeed, even for a=6, it's non-negative.But if a=10, then the expression is sin²x +10 sinx +10 +3= sin²x +10 sinx +13. Let's compute at t=-1/2:(-1/2)^2 +10*(-1/2) +13=0.25 -5 +13=8.25 ≥0. At t=1: 1 +10 +13=24≥0. So indeed, it's non-negative.Therefore, regardless of how large a is, as long as a≥-2, the inequality holds. If a is less than -2, then at t=1, the expression is 2a +4, which becomes negative. Hence, the answer is a≥-2.Therefore, the range of real numbers a is all real numbers greater than or equal to -2. So the answer is ( a in [-2, +infty) ).Final AnswerThe range of ( a ) is boxed{[-2, +infty)}.

✅:To find the range of the real number ( a ) such that the inequality ( sin^2 x + a sin x + a + 3 geq 0 ) holds for all ( x in left[-frac{pi}{6}, frac{pi}{2}right] ), we start by substituting ( t = sin x ). This transforms the inequality into ( t^2 + a t + a + 3 geq 0 ) for all ( t in left[-frac{1}{2}, 1right] ).We analyze the quadratic function ( f(t) = t^2 + a t + a + 3 ). The vertex of this parabola is at ( t = -frac{a}{2} ). We need to ensure the function is non-negative for all ( t ) in the interval (left[-frac{1}{2}, 1right]).1. Case 1: Vertex within the interval (left[-frac{1}{2}, 1right]) - The vertex ( t = -frac{a}{2} ) is within the interval if ( -2 leq a leq 1 ). - The minimum value at the vertex is ( fleft(-frac{a}{2}right) = -frac{a^2}{4} + a + 3 ). - Solving ( -frac{a^2}{4} + a + 3 geq 0 ) gives ( -2 leq a leq 6 ). However, since ( -2 leq a leq 1 ), the valid range is ( -2 leq a leq 1 ).2. Case 2: Vertex to the left of the interval (( -frac{a}{2} < -frac{1}{2} )) - This occurs when ( a > 1 ). - The minimum value is at ( t = -frac{1}{2} ), which is ( fleft(-frac{1}{2}right) = frac{a}{2} + frac{13}{4} ). This is always positive for ( a > 1 ).3. Case 3: Vertex to the right of the interval (( -frac{a}{2} > 1 )) - This occurs when ( a < -2 ). - The minimum value is at ( t = 1 ), which is ( f(1) = 2a + 4 ). This is negative for ( a < -2 ), so no solutions exist here.Combining the valid ranges from all cases, we find that ( a geq -2 ).Thus, the range of the real number ( a ) is (boxed{[-2, +infty)}).

🔑:We are given the inequality (sin^2 x + a sin x + a + 3 geq 0) for all (x in left[-frac{pi}{6}, frac{pi}{2} right]) and we need to find the range of real values of (a) such that the inequality holds.1. Define the function: Let ( f(x) = sin^2 x + a sin x + a + 3 ).2. Transform the function: Using the identity ((sin x + b)^2 = sin^2 x + 2b sin x + b^2 ), we can rewrite (f(x)): [ f(x) = left(sin x + frac{a}{2}right)^2 + a + 3 - frac{a^2}{4} ] Thus, [ f(x) = left(sin x + frac{a}{2}right)^2 + 3 + a - frac{a^2}{4} ]3. Determine the range of (sin x): Since (x in left[-frac{pi}{6}, frac{pi}{2}right]), we have (sin x in left[-frac{1}{2}, 1right]).4. Define a new variable: Let ( t = sin x ). Then (t in left[-frac{1}{2}, 1right]), and the function becomes: [ g(t) = left(t + frac{a}{2}right)^2 + 3 + a - frac{a^2}{4} ]5. Find the minimum of (g(t)): For (g(t)) to be non-negative, its minimum value over the interval (left[-frac{1}{2}, 1right]) must be non-negative.6. Evaluate the boundary points: - Evaluate (g(t)) at (t = -frac{1}{2}): [ gleft(-frac{1}{2}right) = left(-frac{1}{2} + frac{a}{2}right)^2 + 3 + a - frac{a^2}{4} ] Simplify the expression inside the square: [ = left(frac{a - 1}{2}right)^2 + 3 + a - frac{a^2}{4} ] [ = frac{(a-1)^2}{4} + 3 + a - frac{a^2}{4} ] [ = frac{a^2 - 2a + 1}{4} + 3 + a - frac{a^2}{4} ] Combine like terms: [ frac{a^2 - 2a + 1 - a^2}{4} + a + 3 ] [ = -frac{2a - 1}{4} + a + 3 ] [ = -frac{2a - 1}{4} + frac{4a}{4} + 3 ] [ = frac{2a + 1}{4} + 3 ] For (gleft(-frac{1}{2}right) geq 0): [ frac{2a + 1}{4} + 3 geq 0 ] [ frac{2a + 1}{4} geq -3 implies 2a + 1 geq -12 implies 2a geq -13 implies a geq -frac{13}{2} ] - Evaluate (g(t)) at (t = 1): [ g(1) = left(1 + frac{a}{2}right)^2 + 3 + a - frac{a^2}{4} ] Simplify the expression inside the square: [ = left(frac{2 + a}{2}right)^2 + 3 + a - frac{a^2}{4} ] [ = left(frac{2 + a}{2}right)^2 + 3 + a - frac{a^2}{4} ] [ = frac{(2 + a)^2}{4} + 3 + a - frac{a^2}{4} ] [ = frac{4 + 4a + a^2}{4} + 3 + a - frac{a^2}{4} ] [ = 1 + a + frac{a^2}{4} + 3 + a - frac{a^2}{4} ] [ = 4 + 2a ] For (g(1) geq 0): [ 4 + 2a geq 0 ] [ 2a geq -4 implies a geq -2 ]7. Combine the conditions: From evaluating at both boundaries, we have: - If (-frac{1}{2} leq t leq 1), then (a geq -2) - Otherwise, (a geq -frac{13}{2}) Thus, the range consolidates to (a geq -2).Conclusion:[boxed{[-2, +infty)}]Hence, the range of the real values of (a) is ([-2, +infty)).

🧠:Okay, so I need to figure out the probability that hunter B catches more ducks than hunter A. Both hunters hit a duck as often as they miss, which means each has a 50% chance of hitting any duck they encounter. Let me break this down step by step.First, let's understand the problem. Hunter A encountered 50 ducks, and Hunter B encountered 51 ducks. Each time they encounter a duck, they have a 50% chance to hit it (catch it) and a 50% chance to miss. We need the probability that the total number of ducks caught by B is greater than those caught by A.Let me formalize this. Let’s denote:- ( X_A ) as the number of ducks caught by hunter A. Since A encountered 50 ducks, ( X_A ) follows a binomial distribution with parameters ( n = 50 ) and ( p = 0.5 ). So, ( X_A sim text{Binomial}(50, 0.5) ).- Similarly, ( X_B ) is the number of ducks caught by hunter B. Since B encountered 51 ducks, ( X_B sim text{Binomial}(51, 0.5) ).We need to find ( P(X_B > X_A) ).Hmm, okay. So the question is about comparing two binomial variables with different numbers of trials. Since each trial is independent and the probability is the same, maybe there's a symmetry here?Wait, both hunters have the same probability of hitting, 0.5. But hunter B has one more trial (51 vs. 50). So maybe we can use some properties of binomial distributions here.Alternatively, since each hit is a Bernoulli trial with p=0.5, the total hits for each hunter will be like flipping 50 fair coins for A and 51 fair coins for B, counting the number of heads. We want the probability that B gets more heads than A.Alternatively, maybe we can model the difference between their catches. Let's think: ( P(X_B > X_A) = P(X_B - X_A > 0) ).But ( X_B ) and ( X_A ) are independent random variables. The distribution of ( X_B - X_A ) would be the convolution of ( X_B ) and ( -X_A ). However, since they are independent, maybe we can compute the probability by summing over all possible values where ( X_B > X_A ).Yes, that might be the way. So,( P(X_B > X_A) = sum_{k=0}^{50} sum_{m=k+1}^{51} P(X_A = k) P(X_B = m) )But this seems computationally intensive. For each k from 0 to 50, and for each m from k+1 to 51, compute the product of probabilities. That's a lot of terms. Maybe there's a smarter way.Alternatively, since both hunters have p=0.5, perhaps there's a symmetry or combinatorial argument we can use.Wait, let me recall that for two independent binomial variables with the same p, the probability that one is greater than the other can sometimes be simplified. But in this case, the number of trials is different.Let me think. Let’s consider that each hunter's hits can be thought of as a symmetric random walk. But maybe not directly helpful.Alternatively, consider that the total number of trials for both is 50 + 51 = 101. If we imagine all 101 ducks, each hunted by either A or B, with each having a 50% chance of being hit by their respective hunter. Wait, but actually, each duck is only encountered by one hunter. So maybe that's not the right approach.Wait, but perhaps we can model this as a single experiment where we have 50 + 51 = 101 independent Bernoulli trials, 50 with label A and 51 with label B, each with p=0.5. Then, the total catches for A and B are sums over their respective trials. Then, the question is, what's the probability that the sum over B's trials exceeds the sum over A's trials.Alternatively, think of the entire process as a comparison between two independent binomial variables.Alternatively, perhaps using generating functions. The generating function for ( X_A ) is ( (0.5 + 0.5z)^{50} ), and for ( X_B ) is ( (0.5 + 0.5z)^{51} ). The probability generating function for ( X_B - X_A ) would be the product of the generating functions of ( X_B ) and ( -X_A ). But generating functions for differences might be complicated.Alternatively, maybe we can use the fact that for independent variables, the probability that ( X_B > X_A ) is equal to the probability that ( X_B - X_A > 0 ). But how do we compute this?Alternatively, perhaps we can note that since both are binomial, the difference ( X_B - X_A ) is a Skellam distribution if they were Poisson, but they are binomial. However, Skellam applies to Poisson distributions, so maybe not directly applicable here.Alternatively, perhaps we can use normal approximation. For large n, binomial distributions can be approximated by normal distributions. Since 50 and 51 are reasonably large, maybe this is feasible.The mean of ( X_A ) is ( 50 * 0.5 = 25 ), variance ( 50 * 0.5 * 0.5 = 12.5 ).Similarly, the mean of ( X_B ) is ( 51 * 0.5 = 25.5 ), variance ( 51 * 0.25 = 12.75 ).Then, the difference ( X_B - X_A ) would have mean ( 25.5 - 25 = 0.5 ), and variance ( 12.5 + 12.75 = 25.25 ).Therefore, standard deviation is ( sqrt{25.25} approx 5.025 ).Then, the probability that ( X_B - X_A > 0 ) is approximately equal to the probability that a normal variable with mean 0.5 and standard deviation ~5.025 is greater than 0.The Z-score for 0 is ( (0 - 0.5)/5.025 ≈ -0.0995 ).Looking up the Z-table, the probability that Z > -0.0995 is 1 - Φ(-0.0995) = Φ(0.0995) ≈ 0.5398.So approximately 54% chance.But this is an approximation. The question is whether the exact answer is 0.5 or something close. Wait, but with the normal approximation, it's about 54%. However, maybe due to the continuity correction, we should adjust.Wait, the continuity correction for normal approximation would adjust the boundary. Since we're approximating a discrete distribution with a continuous one, we might consider that the probability ( P(X_B > X_A) = P(X_B - X_A geq 1) ). So instead of using 0 as the boundary, we might use 0.5.Thus, the Z-score would be ( (0.5 - 0.5)/5.025 ≈ 0 ). Therefore, the probability would be 0.5. Wait, that can't be. Wait, no:Wait, if we use continuity correction, then:We want ( P(X_B - X_A geq 1) ). In the normal approximation, this is equivalent to ( P(X_B - X_A geq 0.5) ), because in the continuous case, 1 in discrete corresponds to the interval from 0.5 to 1.5. So, using continuity correction, the Z-score would be ( (0.5 - 0.5)/5.025 ≈ 0 ), so the probability is 0.5.But this contradicts the previous calculation. Hmm, perhaps I made a mistake here.Wait, let's clarify. The difference ( D = X_B - X_A ). We need ( P(D > 0) ). Since D is an integer (since both X_B and X_A are integers), ( P(D > 0) = P(D geq 1) ). So applying continuity correction, we approximate this as ( P(D geq 0.5) ).Therefore, the Z-score is ( (0.5 - 0.5)/5.025 = 0 ). So the probability is 0.5.But this seems conflicting. Wait, if we don't use continuity correction, we get approximately 0.54, but with continuity correction, we get 0.5. Which one is more accurate?Wait, the exact answer is likely close to 0.5. But given that hunter B has one more trial, maybe the probability is slightly more than 0.5.Alternatively, let's think about it another way. Imagine that both hunters A and B hunt 50 ducks each. Then, due to symmetry, the probability that B catches more than A is equal to the probability that A catches more than B, and the remaining probability is that they catch the same. So, ( P(X_B > X_A) = P(X_A > X_B) ), and ( P(X_B > X_A) = (1 - P(X_A = X_B))/2 ). So in this case, if they have the same number of trials, the probability would be 0.5*(1 - P(equal)).But in our problem, hunter B has one more duck. So perhaps the probability is slightly more than 0.5.Wait, let's model this. If we have two hunters, A with n trials and B with n+1 trials. Each trial is p=0.5. Then, the probability that B has more successes than A is equal to?Maybe there's a theorem here. Let me recall. If you have two independent binomial variables, X ~ Bin(n, p) and Y ~ Bin(m, p), then P(Y > X) can be calculated using certain recursive formulas or combinatorial identities.Alternatively, here's an idea. Let's consider that B has 51 trials and A has 50. Let's think of B's trials as 50 trials plus one extra trial. Let's denote Y = Y' + Y'', where Y' ~ Bin(50, 0.5) and Y'' ~ Bin(1, 0.5). Then, Y is Bin(51, 0.5).So, we need P(Y > X_A) = P(Y' + Y'' > X_A). Since Y' and X_A are both Bin(50, 0.5) and independent. Let’s denote X_A and Y' as two independent Bin(50, 0.5) variables. Then Y'' is an independent coin flip (0 or 1 with p=0.5).Therefore, the probability becomes:P(Y' + Y'' > X_A) = P(Y' > X_A) + P(Y' = X_A and Y'' = 1)Because if Y' > X_A, then regardless of Y'', Y' + Y'' will be greater. If Y' = X_A, then Y'' needs to be 1 for Y' + Y'' to exceed X_A. If Y' < X_A, then even if Y'' =1, the total would be Y' +1, which could be ≤ X_A.So, breaking it down:P(Y > X_A) = P(Y' > X_A) + 0.5 * P(Y' = X_A)Now, note that since Y' and X_A are identically distributed (both Bin(50, 0.5)), then P(Y' > X_A) = P(X_A > Y') due to symmetry. Let’s denote that as Q.Also, let's denote P(Y' = X_A) as T.Then, since Q + Q + T = 1, because either Y' > X_A, Y' < X_A, or Y' = X_A.Therefore, 2Q + T = 1 => Q = (1 - T)/2.Therefore, substituting back:P(Y > X_A) = Q + 0.5*T = (1 - T)/2 + 0.5*T = (1 - T + T)/2 = 1/2.Wait, that's surprising. So according to this reasoning, the probability is 1/2. But hunter B has an extra trial. How does that reconcile?But wait, in this case, we considered that Y = Y' + Y'' where Y' ~ Bin(50, 0.5) and Y'' ~ Bin(1, 0.5). Then, when we calculated P(Y > X_A), we found that it equals 0.5. So regardless of the extra trial, the probability is 1/2?But that seems counterintuitive. If B has an extra chance, shouldn't the probability be more than 1/2?Wait, let's check this logic again. Let me write it step by step.1. Let Y' ~ Bin(50, 0.5), X_A ~ Bin(50, 0.5), Y'' ~ Bin(1, 0.5), all independent.2. Then, Y = Y' + Y'' ~ Bin(51, 0.5).3. We need P(Y > X_A) = P(Y' + Y'' > X_A).4. Split into two cases: a. If Y' > X_A: Then Y' + Y'' ≥ Y' > X_A, so regardless of Y'' (whether 0 or 1), Y' + Y'' > X_A. So this contributes P(Y' > X_A). b. If Y' = X_A: Then Y' + Y'' > X_A iff Y'' = 1. Since Y'' is 1 with probability 0.5, this contributes 0.5 * P(Y' = X_A). c. If Y' < X_A: Then even if Y'' =1, Y' +1 ≤ X_A only if Y' +1 > X_A. Wait, no. If Y' < X_A, then Y' + Y'' can be either Y' (if Y''=0) or Y' +1 (if Y''=1). So if Y' < X_A, then Y' +1 could be ≤ X_A or > X_A. Wait, but this complicates things.Wait, perhaps my initial breakdown was incorrect.Wait, let me re-express the probability.We have:P(Y > X_A) = P(Y' + Y'' > X_A)= P(Y'' = 1 and Y' >= X_A) + P(Y'' = 0 and Y' > X_A)But that might not be the right way. Alternatively, think:For each possible value of Y' and X_A:If Y' > X_A: Then Y' + Y'' is at least Y', which is already greater than X_A. So whether Y'' is 0 or 1, Y' + Y'' > X_A. So this contributes P(Y' > X_A).If Y' = X_A: Then Y' + Y'' > X_A iff Y'' =1. So contributes 0.5 * P(Y' = X_A).If Y' < X_A: Then Y' + Y'' can be Y' or Y' +1. So in this case, even if Y'' =1, Y' +1 might still be less than or equal to X_A. For example, if Y' = X_A -2, then Y' +1 = X_A -1 < X_A, so even with Y''=1, it's still less. Only when Y' = X_A -1, Y''=1 would make Y' +1 = X_A, which is not greater. Wait, but even then, Y' +1 = X_A is not greater than X_A. So actually, in the case Y' < X_A, even if Y''=1, Y' +1 can never exceed X_A. Because Y' < X_A => Y' +1 <= X_A. Because Y' and X_A are integers.Wait, if Y' < X_A, then Y' <= X_A -1. So Y' +1 <= X_A. Therefore, Y' + Y'' <= X_A when Y' < X_A, since Y'' is 0 or 1.Therefore, in the case Y' < X_A, Y' + Y'' <= X_A. Therefore, in this case, regardless of Y'', we can't have Y' + Y'' > X_A.Therefore, the total probability is:P(Y' > X_A) + 0.5 * P(Y' = X_A)Which is the same as before.Then, since Y' and X_A are independent and identically distributed (both Bin(50, 0.5)), then P(Y' > X_A) = P(X_A > Y') = Q, and P(Y' = X_A) = T.So, as before, 2Q + T =1 => Q = (1 - T)/2.Therefore, P(Y > X_A) = (1 - T)/2 + 0.5 * T = (1 - T + T)/2 = 1/2.Wow, so according to this, even though B has an extra trial, the probability is 1/2? That seems counterintuitive. How is that possible?Wait, let me test this with a simpler case. Let’s take n=1 for A and n=2 for B. So A has 1 trial, B has 2 trials. What is P(B > A)?Let's compute it manually.A can have 0 or 1.B can have 0,1,2.Compute all possibilities:Case 1: A=0 (prob 0.5)Then B needs to have at least 1. P(B >=1) = 1 - P(B=0) = 1 - 0.25 = 0.75Case 2: A=1 (prob 0.5)Then B needs to have at least 2. P(B >=2) = 0.25Therefore, total probability: 0.5 * 0.75 + 0.5 * 0.25 = 0.375 + 0.125 = 0.5.So it's exactly 0.5. Huh. So even in this case, where B has an extra trial, the probability that B > A is 0.5.That's surprising. So according to this, regardless of the number of trials, as long as B has n+1 trials and A has n trials, the probability that B > A is 0.5.But how is that possible? Let's test another example. Suppose A has 0 trials and B has 1 trial. Then P(B > A) is P(B=1) * P(A=0) + P(B >=1) * P(A=0). Wait, A has 0 trials, so A=0 always. So P(B > A) = P(B >=1) = 0.5. So again 0.5.Wait, but in this case, if A has 0 trials, B just needs to have at least 1, which is 0.5. So again, 0.5. So this seems to hold.Alternatively, if A has 2 trials and B has 3 trials. Then, using the same logic, P(B > A) = 0.5.Wait, but how?Let me compute it manually for small numbers.A has 2 trials, B has 3 trials. Let's compute P(B > A):Possible values for A: 0,1,2.Possible values for B: 0,1,2,3.Compute the probability:For A=0: B needs >=1. Probability is (0.5)^2 * [1 - (0.5)^3] = (1/4) * (1 - 1/8) = (1/4)(7/8) = 7/32.For A=1: B needs >=2. Probability is C(2,1)(0.5)^2 * [C(3,2)(0.5)^3 + C(3,3)(0.5)^3] = 2*(1/4) * [3*(1/8) + 1*(1/8)] = (1/2) * (4/8) = (1/2)(1/2) = 1/4. So 1/4.For A=2: B needs >=3. Probability is C(2,2)(0.5)^2 * C(3,3)(0.5)^3 = (1/4)*(1/8) = 1/32.Total probability: 7/32 + 1/4 + 1/32 = 7/32 + 8/32 + 1/32 = 16/32 = 0.5.Again, 0.5. Wow. So this seems to hold generally. So the probability that a Bin(n+1, 0.5) is greater than a Bin(n, 0.5) is 0.5.Therefore, regardless of n, as long as the hunters have n and n+1 trials with p=0.5, the probability is 0.5. So in the original problem, the answer is 1/2.But why is this the case? It seems counterintuitive because B has an extra trial, but the symmetry comes in because the extra trial is a fair coin flip.Wait, from the earlier breakdown:P(Y > X_A) = P(Y' > X_A) + 0.5 * P(Y' = X_A)But since Y' and X_A are identically distributed, P(Y' > X_A) = P(X_A > Y') = Q, and P(Y' = X_A) = T. Then, since Q + Q + T =1, Q = (1 - T)/2.Thus, P(Y > X_A) = (1 - T)/2 + 0.5 * T = 0.5.Therefore, the probability is always 0.5, regardless of n. This is because the extra trial is symmetric. The key idea is that the extra trial (Y'') gives a 50% chance to add 1, which perfectly balances the probability between the two cases where Y' > X_A and Y' = X_A.Hence, the probability that B's catch exceeds A's catch is 1/2.But let me verify this with another perspective. Suppose we consider all possible outcomes of A's 50 ducks and B's 51 ducks. Each duck is a fair coin flip. Now, consider pairing B's first 50 trials with A's 50 trials. For each of these 50 pairs, the probability that B's trial in the pair results in more hits than A's is symmetric. Then, B has one extra trial, which is independent. So the total excess of B over A is the excess from the 50 paired trials plus the result of the 51st trial.But the excess from the paired trials is symmetric around 0, so the probability that the total excess plus the 51st trial is positive is 0.5. Because the 51st trial is equally likely to be a hit or miss, and if the excess from the first 50 is zero, then the 51st trial decides it. If the excess is positive, it's already a win, and if it's negative, it's a loss. But the probability of positive excess equals the probability of negative excess, so adding the 51st trial which is independent and fair, balances it out to 0.5.Therefore, regardless of the number of trials, as long as B has one more trial than A, and each trial is fair, the probability is 0.5.Therefore, the answer is 1/2.But wait, the original problem is phrased as "hunter B's catch exceeds hunter A's catch". So if they have the same number of catches, it doesn't count. So the probability is exactly 0.5.Therefore, the final answer is 1/2, or 50%.But this seems too clean. Let me check with n=1 and m=2 again.If A has 1 trial, B has 2 trials. The probability that B > A is 0.5, as computed earlier. Similarly, if A has 0 trials and B has 1, it's 0.5.Alternatively, let's think about the difference between B and A. Since B has an extra trial, which is a Bernoulli(0.5), then the difference D = (Y' - X_A) + Y'' where Y' ~ Bin(50, 0.5), X_A ~ Bin(50, 0.5), and Y'' ~ Bernoulli(0.5). Then, Y' - X_A is symmetric around 0, so adding Y'' which is +1 with probability 0.5 and 0 otherwise. Then, the total difference D is symmetric in a way that the probability D > 0 is 0.5.Alternatively, the process can be seen as follows: imagine both hunters A and B hunt 50 ducks each, and then B hunts one more duck. The comparison between the first 50 ducks of B and A's 50 is symmetric, so the probability B is ahead after 50 is equal to the probability A is ahead, and the probability they are equal is T. Then, the extra duck gives B a 50% chance to increment if they were equal. Therefore, the total probability B > A is equal to the probability B was ahead after 50 plus half the probability they were equal. But since after 50, the probability B is ahead is equal to the probability A is ahead, which gives each as (1 - T)/2, then total probability is (1 - T)/2 + T/2 = 1/2.Therefore, no matter what, it's 1/2.Thus, the answer is 1/2.But let me confirm with a different approach. Let’s consider all possible outcomes for A and B. Each outcome is a pair (a, b) where a is the number of hits by A and b by B. The probability is C(50, a) * (0.5)^50 * C(51, b) * (0.5)^51.We need to sum over all a and b where b > a.Alternatively, note that the joint distribution is symmetric in a certain way. Let's swap A and B for the first 50 trials. Wait, not exactly, since B has one more trial.Alternatively, consider that for each sequence of outcomes for A and B's first 50 trials, they are equally likely. The extra trial for B is independent. So for each outcome where A's 50 trials result in a and B's first 50 result in b', then B's total is b' + b'' where b'' is 0 or 1.Therefore, the comparison between a and b' + b''.If we fix a and b', then:If b' > a: B wins.If b' = a: B wins if b'' =1.If b' < a: B loses.Now, since A's 50 and B's first 50 are symmetric, for each a and b', the probability that b' > a is equal to the probability that a > b'. Let’s denote this as Q. The probability that b' = a is T.Thus, the total probability that B wins is Q + 0.5*T.But since Q = probability b' > a = probability a > b' = Q, and Q + Q + T =1, then Q = (1 - T)/2.Thus, total probability is (1 - T)/2 + T/2 = 1/2.Hence, regardless of T, the total probability is 1/2.Therefore, the answer is 1/2.This seems to be a general result when comparing Bin(n, 0.5) and Bin(n+1, 0.5). The probability that Bin(n+1, 0.5) exceeds Bin(n, 0.5) is exactly 0.5.Therefore, the probability that hunter B's catch exceeds hunter A's catch is 1/2.Final AnswerThe probability that hunter B's catch exceeds hunter A's catch is boxed{dfrac{1}{2}}.

✅:To determine the probability that hunter B's catch exceeds hunter A's catch, we start by noting that each hunter hits a duck with a probability of 0.5. Hunter A encountered 50 ducks, and hunter B encountered 51 ducks. We denote the number of ducks caught by A and B as X_A sim text{Binomial}(50, 0.5) and X_B sim text{Binomial}(51, 0.5), respectively. We need to find P(X_B > X_A).Key steps and reasoning:1. Symmetry and Decomposition: - Consider X_B as the sum of two independent random variables: Y' sim text{Binomial}(50, 0.5) and Y'' sim text{Bernoulli}(0.5). Thus, X_B = Y' + Y''. - We need P(Y' + Y'' > X_A). This can be decomposed into two cases: - If Y' > X_A, then Y' + Y'' will certainly be greater than X_A. - If Y' = X_A, then Y' + Y'' will be greater than X_A if Y'' = 1 (probability 0.5).2. Probability Analysis: - Let Q = P(Y' > X_A) and T = P(Y' = X_A). Due to symmetry, Y' and X_A are identically distributed, so P(Y' > X_A) = P(X_A > Y') = Q and 2Q + T = 1. - Therefore, Q = frac{1 - T}{2}.3. Combining Probabilities: - The probability P(Y' + Y'' > X_A) is given by Q + 0.5T. - Substituting Q = frac{1 - T}{2}, we get: [ P(Y' + Y'' > X_A) = frac{1 - T}{2} + 0.5T = frac{1 - T + T}{2} = frac{1}{2} ]4. Conclusion: - The probability that hunter B's catch exceeds hunter A's catch is exactly frac{1}{2}, due to the symmetry and the fair coin flip nature of the extra trial.Thus, the probability that hunter B's catch exceeds hunter A's catch is boxed{dfrac{1}{2}}.

🔑:1. Understanding the problem setup: - Two hunters, ( A ) and ( B ), are hunting ducks. - Each has a probability of hitting (or missing) a duck, both being equal and independent of the other, specifically ( frac{1}{2} ). - Hunter ( A ) encounters 50 ducks. - Hunter ( B ) encounters 51 ducks.2. Translating the problem into probability terms: - The problem can be modeled as each hunter flipping a fair coin for each duck seen. - Hunter ( A ) flips a coin 50 times. - Hunter ( B ) flips a coin 51 times. - We need to find the probability that the number of heads for ( B )'s flips is greater than the number of heads for ( A )'s flips.3. Setting up the equivalency: - Let ( X_A ) be the number of heads obtained by ( A ) in 50 flips. - Let ( X_B ) be the number of heads obtained by ( B ) in 51 flips. - We need to calculate ( P(X_B > X_A) ).4. Analyzing the outcomes: - The event ( X_B > X_A ) is complementary to ( X_A geq X_B ) because the two cover all possible outcomes. - Considering the symmetry in binomial distribution where each flip has a probability ( frac{1}{2} ) of being heads or tails, the outcomes are equally likely.5. Breaking down the sample space: - The total possible outcomes are divided into two parts: 1. Outcomes where ( X_B ) results in more heads than ( X_A ). 2. Outcomes where ( X_B ) results in equal or fewer heads than ( X_A ).6. Considering symmetry and equal chances: - Due to the coin flips being fair, the number of favorable outcomes for ( X_B > X_A ) is equal to the number of unfavorable outcomes. - Therefore, we leverage the idea that both being equally probable, the probability ( P(X_B > X_A) ) is equal to the probability ( P(X_A geq X_B) ).7. Calculating the probabilities: - The problem then simplifies to finding that the favorable and unfavorable counts are symmetric in this binomial setup. - Therefore, [ P(X_B > X_A) = frac{1}{2}. ] Conclusion:Thus, the probability that hunter ( B ) will have a higher amount of ducks than hunter ( A ) is [boxed{frac{1}{2}}.]

🧠:Okay, so I need to find the remainders when the polynomial f(x) = x²⁴³ + x⁸¹ + x²⁷ + x⁹ + x³ + 1 is divided by two different divisors: part a) is x - 1, and part b) is x² - 1. Let me start with part a) because it seems simpler.For part a), when dividing a polynomial by x - 1, the remainder is just the value of the polynomial evaluated at x = 1. I remember that from the Remainder Theorem. So, all I need to do is plug in 1 into f(x) and compute the result. Let's check that.f(1) = 1²⁴³ + 1⁸¹ + 1²⁷ + 1⁹ + 1³ + 1. Since any number to any power is still 1, each term here is 1. Let's count how many terms there are: x²⁴³, x⁸¹, x²⁷, x⁹, x³, and 1. That's six terms. So, adding them up: 1 + 1 + 1 + 1 + 1 + 1 = 6. Therefore, the remainder when f(x) is divided by x - 1 is 6. That seems straightforward.Now, moving on to part b), which is dividing by x² - 1. The remainder here should be a first-degree polynomial, since the divisor is degree 2. The general form would be ax + b, where a and b are constants we need to find. To find the remainder when dividing by x² - 1, we can use polynomial remainder theorem or utilize the fact that x² ≡ 1 modulo x² - 1. Therefore, we can replace x² with 1 in the polynomial to simplify it.Wait, let me think again. Since x² ≡ 1 mod (x² - 1), then x³ = x² * x ≡ 1 * x = x, x⁴ = x² * x² ≡ 1 * 1 = 1, and so on. So higher powers of x can be reduced by replacing x² with 1. Therefore, exponents can be simplified modulo 2. For example, xⁿ ≡ x^(n mod 2). But wait, that's only if n is even or odd. If the exponent is even, it becomes 1, and if it's odd, it becomes x. But let's verify that.Let me consider an example: x³ = x² * x ≡ 1 * x = x. Similarly, x⁴ = (x²)² ≡ 1² = 1. So, for exponents, if it's even, it becomes 1; if it's odd, it becomes x. But in our polynomial f(x), all exponents are powers of 3. Let's list them: 243, 81, 27, 9, 3, and 1. Wait, hold on, 243 is 3⁵, 81 is 3⁴, 27 is 3³, 9 is 3², 3 is 3¹, and the last term is 1, which is x⁰. Hmm, all exponents except the last term are multiples of 3. So each exponent is 3^k where k ranges from 0 to 5? Wait, no. 243 is 3^5, 81 is 3^4, 27 is 3^3, 9 is 3^2, 3 is 3^1, and 1 is 3^0. So each term is x^(3^k) for k from 0 to 5. Interesting.So when we reduce each term modulo x² - 1, which allows us to replace x² with 1. Let's see how each exponent can be reduced.First, let's note that x² ≡ 1 mod (x² -1). Therefore, x^(2m + r) ≡ (x²)^m * x^r ≡ 1^m * x^r ≡ x^r mod (x² -1). So, exponents can be reduced modulo 2. So, for any exponent n, we can write n = 2m + r, where r is 0 or 1. Then x^n ≡ x^r. So, if the exponent is even, it's equivalent to 1, and if odd, equivalent to x.But in our case, all the exponents in f(x) are 3^k. Let's compute each exponent modulo 2:3^0 = 1: 1 mod 2 = 1 (odd)3^1 = 3: 3 mod 2 = 1 (odd)3^2 = 9: 9 mod 2 = 1 (odd)3^3 = 27: 27 mod 2 = 1 (odd)3^4 = 81: 81 mod 2 = 1 (odd)3^5 = 243: 243 mod 2 = 1 (odd)Wait a minute! All the exponents in f(x) except the last term (which is x^0) are 3^k, which are all odd numbers. Because 3 is odd, and any power of an odd number is odd. So each exponent 3^k is odd. Therefore, when we reduce x^(3^k) modulo x² -1, each of these terms becomes x^1, since exponents are odd. Therefore, x^(3^k) ≡ x mod (x² -1). So, each term except the constant term 1 will be x. Let's check that.So f(x) modulo x² -1 would be:x²⁴³ ≡ x^(odd) ≡ xx⁸¹ ≡ xx²⁷ ≡ xx⁹ ≡ xx³ ≡ xand the constant term 1 remains 1.Therefore, adding them up:x + x + x + x + x + 1 = 5x + 1.Wait, but let me count the number of terms. The original polynomial has 6 terms: x²⁴³, x⁸¹, x²⁷, x⁹, x³, and 1. Each of the first five terms (x²⁴³ to x³) are odd exponents, so each reduces to x, and the last term is 1. Therefore, 5x + 1. So the remainder would be 5x + 1. But let me verify this because I might have made a mistake.Wait, let's do it step by step for each term:1. x²⁴³: 243 divided by 2 is 121 with remainder 1. So x²⁴³ ≡ x^1 = x2. x⁸¹: 81 divided by 2 is 40 with remainder 1. So x⁸¹ ≡ x^1 = x3. x²⁷: 27 divided by 2 is 13 with remainder 1. So x²⁷ ≡ x4. x⁹: 9 divided by 2 is 4 with remainder 1. So x⁹ ≡ x5. x³: 3 divided by 2 is 1 with remainder 1. So x³ ≡ x6. The last term is 1, so remains 1.Therefore, adding them all up: x + x + x + x + x + 1 = 5x + 1. Therefore, the remainder is 5x + 1. That seems correct.But let me check this with another method to be sure. Another way is to use polynomial division or use the Remainder Factor Theorem for divisors of higher degree. For a divisor of degree 2, the remainder will be of degree less than 2, so R(x) = ax + b. To find a and b, we can evaluate f(x) at the roots of the divisor x² - 1, which are x = 1 and x = -1. Then, plugging these into f(x) should give the same result as plugging them into R(x). So f(1) = R(1) and f(-1) = R(-1).We already computed f(1) in part a) as 6. So R(1) = a*1 + b = a + b = 6.Now compute f(-1):f(-1) = (-1)^243 + (-1)^81 + (-1)^27 + (-1)^9 + (-1)^3 + 1.Each of these terms: (-1)^odd = -1, and the last term is 1. Let's compute each term:(-1)^243: since 243 is odd, this is -1Similarly, (-1)^81 = -1(-1)^27 = -1(-1)^9 = -1(-1)^3 = -1And the last term is 1.So adding them up: (-1) + (-1) + (-1) + (-1) + (-1) + 1 = -5 + 1 = -4.Therefore, f(-1) = -4. But R(-1) = a*(-1) + b = -a + b. So:We have two equations:1) a + b = 62) -a + b = -4We can solve this system of equations. Let's subtract the second equation from the first:(a + b) - (-a + b) = 6 - (-4)a + b + a - b = 102a = 10 => a = 5Substitute a = 5 into the first equation:5 + b = 6 => b = 1Therefore, the remainder is 5x + 1, which matches our previous result. So that's consistent.Therefore, for part b), the remainder is 5x + 1.Wait, just to make sure, let's try another approach. Let's express f(x) as (x² - 1) * Q(x) + ax + b. Then, if we substitute x = 1 and x = -1, we should get the same results as before. We already did that, so that's why we get the equations. So that's another confirmation. Therefore, confident that remainder is 5x + 1.But let me check with a small example. Suppose we have a simpler polynomial, say x³ + x + 1 divided by x² -1. Then, x³ ≡ x, so x³ + x + 1 ≡ x + x + 1 = 2x + 1. The remainder is 2x + 1. Let's verify with Remainder Theorem: f(1) = 1 + 1 + 1 = 3, and f(-1) = -1 + (-1) + 1 = -1. Then equations: a + b = 3 and -a + b = -1. Solving gives a = 2, b = 1. Correct. So that method works.Therefore, our approach for part b) is correct. So, final answers: a) 6, b) 5x + 1.But let me just recap:For a) Remainder when divided by x -1 is f(1) = 6.For b) Remainder is 5x + 1, confirmed by two methods: substituting x = 1 and x = -1 into f(x) and solving for the remainder coefficients, and also by reducing each term modulo x² -1.So, I think that's solid. No contradictions in the reasoning. Thus, the answers are a) 6 and b) 5x + 1.Final Answera) boxed{6}b) boxed{5x + 1}

✅:To find the remainders when the polynomial ( f(x) = x^{243} + x^{81} + x^{27} + x^{9} + x^{3} + 1 ) is divided by ( x - 1 ) and ( x^2 - 1 ): Part a) Remainder when divided by ( x - 1 )Using the Remainder Theorem, the remainder is the value of the polynomial evaluated at ( x = 1 ):[f(1) = 1^{243} + 1^{81} + 1^{27} + 1^{9} + 1^{3} + 1 = 1 + 1 + 1 + 1 + 1 + 1 = 6]Thus, the remainder is (boxed{6}). Part b) Remainder when divided by ( x^2 - 1 )The remainder will be a first-degree polynomial ( ax + b ). Using the polynomial remainder theorem, we evaluate ( f(x) ) at the roots of ( x^2 - 1 ), which are ( x = 1 ) and ( x = -1 ).1. For ( x = 1 ):[f(1) = 6 implies a(1) + b = a + b = 6]2. For ( x = -1 ):[f(-1) = (-1)^{243} + (-1)^{81} + (-1)^{27} + (-1)^9 + (-1)^3 + 1 = -1 - 1 - 1 - 1 - 1 + 1 = -4]This gives the equation:[a(-1) + b = -a + b = -4]Solving the system of equations:[begin{cases}a + b = 6 -a + b = -4end{cases}]Subtracting the second equation from the first:[2a = 10 implies a = 5]Substituting ( a = 5 ) into ( a + b = 6 ):[5 + b = 6 implies b = 1]Thus, the remainder is ( 5x + 1 ), so the answer is (boxed{5x + 1}).

🔑:# Part a):Step 1: Use the Remainder Theorem. The Remainder Theorem states that if a polynomial f(x) is divided by (x - c), then the remainder of this division is f(c).Step 2: According to the Remainder Theorem, to find the remainder when f(x) is divided by (x - 1), evaluate f(1).Step 3: Evaluate the polynomial f(x) at x = 1:[f(1) = 1^{243} + 1^{81} + 1^{27} + 1^9 + 1^3 + 1]Step 4: Solve the expression:[1^{243} = 1, quad 1^{81} = 1, quad 1^{27} = 1, quad 1^9 = 1, quad 1^3 = 1, quad text{and} quad 1 = 1][f(1) = 1 + 1 + 1 + 1 + 1 + 1 = 6]Conclusion: The remainder when f(x) is divided by x - 1 is 6.[boxed{6}]# Part b):Step 1: Note that x^2 - 1 = (x - 1)(x + 1). We need to find the remainder when f(x) is divided by x^2 - 1.Step 2: To simplify, recognize that x^2 - 1 divides polynomials by checking the form ((x^k - x)) where (k) is an integer. If k is an odd multiple of 2, then this will help decompose the polynomial.Step 3: Rewrite f(x) as follows:[f(x) = x^{243} + x^{81} + x^{27} + x^{9} + x^{3} + 1]Step 4: Express f(x) by grouping terms that form multiples of (x^2 - 1):[f(x) = (x^{243} - x) + (x^{81} - x) + (x^{27} - x) + (x^{9} - x) + (x^{3} - x) + (5x + 1)]Step 5: Notice that each term inside the parentheses when simplified goes to x(x^{242} - 1) + x(x^{80} - 1) + x(x^{26} - 1) + x(x^8 - 1) + x(x^2 - 1) which is divisible by x^2 - 1:[(x^{243} - x), (x^{81} - x), (x^{27} - x), (x^{9} - x), (x^{3} - x) quad text{are divisible by} quad (x^2 - 1)]Step 6: Thus, they contribute 0 to the remainder and we are left with the term (5x + 1).Conclusion: The remainder when f(x) is divided by x^2 - 1 is 5x + 1.[boxed{5x + 1}]

🧠:Okay, so I need to figure out if there's an angle α between 0 and π/2 (which is 0 to 90 degrees) such that sin α, cos α, tan α, and cot α can be arranged in some order to form consecutive terms of an arithmetic progression. Hmm, arithmetic progression means that the difference between consecutive terms is constant. Let me start by recalling the definitions and properties of these trigonometric functions.First, let's note that in an arithmetic progression (AP), the difference between consecutive terms is constant. So if we have four terms a, b, c, d in AP, then b - a = c - b = d - c. Which implies that 2b = a + c, 2c = b + d, and so on. Another way to look at it is that the terms must be equally spaced. So, the middle terms are averages of their neighbors.Given that we have four terms here: sin α, cos α, tan α, cot α. We need to arrange them in some order such that they form an AP. Let me list the possible orders. But since there are 4 terms, there are 4! = 24 possible permutations. That's a lot, but maybe we can narrow it down by considering the relationships between these functions.First, let's note some properties:1. For α ∈ (0, π/2), all the functions sin α, cos α, tan α, cot α are positive.2. tan α = sin α / cos α3. cot α = cos α / sin α = 1 / tan α4. Also, sin α and cos α are between 0 and 1, while tan α and cot α can be greater than 1 or less than 1 depending on α. Specifically, if α is in (0, π/4), then tan α < 1 and cot α > 1. If α is in (π/4, π/2), then tan α > 1 and cot α < 1. At α = π/4, tan α = cot α = 1, but sin α = cos α = √2/2 ≈ 0.707. But since α is in (0, π/2), excluding π/4, except when considering equality.So, depending on whether α is less than or greater than π/4, the order of these values changes. Let's consider two cases: α < π/4 and α > π/4.Case 1: α ∈ (0, π/4)In this case, tan α < 1 and cot α > 1. Also, sin α < cos α because in (0, π/4), cosine is larger than sine. So, the order from smallest to largest would be: sin α, tan α, cos α, cot α. Wait, let's verify:tan α = sin α / cos α. Since sin α < cos α here, tan α < 1. Also, cot α = 1 / tan α > 1. So, sin α < tan α < 1 < cot α and cos α is between sin α and 1. Wait, cos α is greater than sin α but less than 1. So the order would be sin α, tan α, cos α, cot α. Wait, but is tan α less than cos α?Let's take a specific example: let α = 30 degrees (π/6 radians). Then sin 30° = 0.5, cos 30° ≈ 0.866, tan 30° ≈ 0.577, cot 30° ≈ 1.732. So, ordering them: sin α = 0.5, tan α ≈ 0.577, cos α ≈ 0.866, cot α ≈ 1.732. So indeed, sin < tan < cos < cot. So in this case, the order is sin α, tan α, cos α, cot α.Case 2: α ∈ (π/4, π/2)Here, tan α > 1 and cot α < 1. Also, sin α > cos α. So, ordering them: cot α, cos α, sin α, tan α. Let's check with α = 60 degrees (π/3 radians). sin 60° ≈ 0.866, cos 60° = 0.5, tan 60° ≈ 1.732, cot 60° ≈ 0.577. So ordering: cot α ≈ 0.577, cos α = 0.5, sin α ≈ 0.866, tan α ≈ 1.732. Wait, that's not correct. Wait, cos 60° is 0.5, which is less than cot 60° ≈ 0.577? No, 0.5 < 0.577. So actually, the order would be cos α, cot α, sin α, tan α. Wait, cos 60° = 0.5, cot 60° ≈ 0.577, sin 60° ≈ 0.866, tan 60° ≈ 1.732. So yes, cos < cot < sin < tan. So in this case, the order is cos α, cot α, sin α, tan α.So depending on the quadrant, the order changes. But regardless, we can see that in both cases, tan and cot are at the ends, either the highest or the lowest. Wait, in the first case, cot is the highest, and in the second case, tan is the highest.But in an arithmetic progression, the terms must be equally spaced. So the difference between consecutive terms is constant. So, if we have four terms a, b, c, d in AP, then d = a + 3k, where k is the common difference.But given that tan and cot are reciprocals, perhaps there's a relationship there. Let me think.Alternatively, perhaps we can set up equations based on possible orderings.But since there are 24 permutations, it's impractical to check all. Maybe we can consider possible positions for tan and cot, given that they are reciprocals.But let's think: in an AP, the average of the first and fourth terms is equal to the average of the second and third terms. So, for four terms a, b, c, d in AP, we have a + d = b + c.Similarly, the sum of all four terms would be 2(a + d) = 2(b + c). But since there are four terms, the sum is a + b + c + d = 4 times the average of the first and last terms.But maybe instead of considering permutations, we can look for relationships between the functions.Given that tan α = sin α / cos α and cot α = cos α / sin α, we can note that tan α * cot α = 1.So, the product of tan and cot is 1, which might be useful.Also, since sin^2 α + cos^2 α = 1.So, maybe if we can express all terms in terms of sin α and cos α, and then set up equations based on the arithmetic progression.Let me denote s = sin α, c = cos α, t = tan α = s/c, k = cot α = c/s.We need to arrange these four numbers s, c, s/c, c/s in some order such that they form an arithmetic progression.So, the four terms must be in AP. Let me suppose that the terms are arranged in ascending order. Since we have two cases (α < π/4 and α > π/4), maybe we can handle both cases.But perhaps it's better to assume an order and set up equations.Alternatively, perhaps the four terms can be arranged such that the middle two terms average to the same as the first and last. For four terms in AP, the sum of the first and fourth terms equals the sum of the second and third terms.So, if we suppose that the four terms in some order are a, b, c, d with a < b < c < d, then a + d = b + c.Moreover, the common difference k would satisfy b = a + k, c = a + 2k, d = a + 3k.So, for four terms, if we can assign variables accordingly, maybe we can find a system of equations.Alternatively, maybe we can assign the four terms as a, a + k, a + 2k, a + 3k, and see if these can correspond to s, c, t, k in some permutation.But given that s and c are between 0 and 1, and t and k are either both greater than 1 or one greater and one less depending on α. Wait, no: if α < π/4, t = tan α < 1 and k = cot α > 1. If α > π/4, t = tan α > 1 and k = cot α < 1. At α = π/4, t = k = 1, but then s = c = √2/2, so all four terms would be s, s, 1, 1, which is not an arithmetic progression unless all terms are equal, which they aren't. So α ≠ π/4.So, depending on whether α is less than or greater than π/4, the terms t and k switch between being less than or greater than 1. So, in either case, two terms are less than 1 (for α < π/4: s, t, c; wait, no: s, c are between 0 and 1, t <1, k >1. So three terms less than 1? Wait, s and c are always between 0 and 1. For α < π/4: s < c <1, t = s/c <1, since s < c. Then k = c/s >1. So, three terms less than 1: s, t, c, and one term greater than 1: k. Similarly, for α > π/4: s > c, so t = s/c >1, k = c/s <1. So in this case, two terms greater than 1: s, t; wait no: s and c are still between 0 and 1. So, for α > π/4: s > c, t = s/c >1, k = c/s <1. So, terms are c, k, s, t. So, two terms less than 1 (c, k), and two terms (s, t) where s is between c and 1, and t is greater than 1.Therefore, in either case, we have two terms less than 1 (s, c in one case, c, k in the other) and two terms where one is between some values and the other is greater than 1. Hmm, maybe this isn't the most productive line of thought.Alternatively, let's note that in an arithmetic progression of four terms, the difference between the first and fourth term is 3 times the common difference. So, if we have the four terms arranged in order, the largest term minus the smallest term is 3k, where k is the common difference. So, perhaps we can set up equations based on this.Let me try considering possible orderings.Case 1: α ∈ (0, π/4). As we saw earlier, the order from smallest to largest is sin α, tan α, cos α, cot α.So, let's suppose that the four terms in AP are sin α, tan α, cos α, cot α. Then, according to AP, the differences between consecutive terms should be equal.So, tan α - sin α = cos α - tan α = cot α - cos α.So, first, tan α - sin α = cos α - tan α.Let me write this equation:tan α - sin α = cos α - tan αBring all terms to one side:tan α - sin α - cos α + tan α = 02 tan α - sin α - cos α = 0Express tan α as sin α / cos α:2 (sin α / cos α) - sin α - cos α = 0Multiply through by cos α to eliminate denominators:2 sin α - sin α cos α - cos^2 α = 0Let's factor sin α:sin α (2 - cos α) - cos^2 α = 0Hmm, not sure. Alternatively, write everything in terms of sin α and cos α:2 sin α / cos α - sin α - cos α = 0Multiply through by cos α:2 sin α - sin α cos α - cos^2 α = 0Let me note that sin α cos α can be written as (sin 2α)/2, but not sure if that helps.Alternatively, let's factor:2 sin α - sin α cos α - cos^2 α = 0Let me factor terms:sin α (2 - cos α) - cos^2 α = 0Hmm, maybe rearrange:sin α (2 - cos α) = cos^2 αLet me divide both sides by cos^2 α (assuming cos α ≠ 0, which it isn't in (0, π/2)):tan α (2 - cos α) = 1So,tan α = 1 / (2 - cos α)But tan α is sin α / cos α, so:sin α / cos α = 1 / (2 - cos α)Multiply both sides by cos α (2 - cos α):sin α (2 - cos α) = cos αExpand the left side:2 sin α - sin α cos α = cos αBring all terms to the left:2 sin α - sin α cos α - cos α = 0Factor terms:sin α (2 - cos α) - cos α = 0Wait, this seems like we're going in circles. Let's see if we can express everything in terms of sin or cos.Let me use the identity sin^2 α + cos^2 α = 1. Let's denote x = cos α. Then sin α = sqrt(1 - x^2).So, substituting into the equation:2 sqrt(1 - x^2) - sqrt(1 - x^2) x - x = 0Factor sqrt(1 - x^2):sqrt(1 - x^2) (2 - x) - x = 0Bring the x to the other side:sqrt(1 - x^2) (2 - x) = xSquare both sides to eliminate the square root:(1 - x^2)(2 - x)^2 = x^2Expand the left side:First, expand (2 - x)^2 = 4 - 4x + x^2Multiply by (1 - x^2):(1 - x^2)(4 - 4x + x^2) = x^2Multiply term by term:1*(4 - 4x + x^2) - x^2*(4 - 4x + x^2) = x^2So,4 - 4x + x^2 - 4x^2 + 4x^3 - x^4 = x^2Combine like terms:4 - 4x + (x^2 - 4x^2) + 4x^3 - x^4 = x^2Simplify:4 - 4x - 3x^2 + 4x^3 - x^4 = x^2Bring all terms to the left:4 - 4x - 3x^2 + 4x^3 - x^4 - x^2 = 0Combine like terms:4 - 4x - 4x^2 + 4x^3 - x^4 = 0Rearranged:-x^4 + 4x^3 - 4x^2 - 4x + 4 = 0Multiply both sides by -1:x^4 - 4x^3 + 4x^2 + 4x - 4 = 0So, we have a quartic equation: x^4 - 4x^3 + 4x^2 + 4x - 4 = 0This looks complicated. Let's see if we can factor it.Let me attempt rational roots using Rational Root Theorem. Possible rational roots are ±1, ±2, ±4.Testing x=1: 1 - 4 + 4 + 4 - 4 = 1 -4 +4 +4 -4 = 1. Not zero.x=2: 16 - 32 + 16 + 8 -4 = 16 -32= -16 +16=0 +8=8 -4=4. Not zero.x= -1: 1 +4 +4 -4 -4 = 1. Not zero.x=4: 256 - 256 + 64 + 16 -4 = 256-256=0 +64=64 +16=80 -4=76. Not zero.So, no rational roots. Hmm. Maybe factor by grouping.x^4 -4x^3 +4x^2 +4x -4Let me group terms:(x^4 -4x^3) + (4x^2 +4x) -4Factor x^3 from first group: x^3(x -4) + 4x(x +1) -4Not helpful. Alternatively:x^4 -4x^3 +4x^2 +4x -4 = (x^4 -4x^3 +4x^2) + (4x -4)Factor x^2 from first group: x^2(x^2 -4x +4) +4(x -1) = x^2(x-2)^2 +4(x -1)Still not helpful. Maybe try to factor as quadratic in x^2.Alternatively, use substitution. Let me set y = x^2. But the equation is x^4 -4x^3 +4x^2 +4x -4=0, which includes x^3 and x terms, so substitution might not work.Alternatively, try to factor into two quadratics:(x^2 + a x + b)(x^2 + c x + d) = x^4 -4x^3 +4x^2 +4x -4Multiply out:x^4 + (a + c)x^3 + (b + d + a c)x^2 + (a d + b c)x + b d = x^4 -4x^3 +4x^2 +4x -4Set up equations:1. a + c = -42. b + d + a c = 43. a d + b c = 44. b d = -4We need to find integers a, b, c, d satisfying these equations.From equation 4: b d = -4. Possible integer pairs (b, d): (1, -4), (-1, 4), (2, -2), (-2, 2), (4, -1), (-4, 1)Let me try b=2, d=-2. Then equation 4 is satisfied: 2*(-2)=-4.Then equation 1: a + c = -4Equation 2: 2 + (-2) + a c = 0 + a c = 4 → a c =4Equation 3: a*(-2) + 2*c = -2a + 2c =4 → -2a + 2c =4 → -a + c =2From equation 1: a + c = -4We have:-a + c = 2a + c = -4Adding both equations:2c = -2 → c = -1Then a = -4 -c = -4 -(-1) = -3Check equation 2: a c = (-3)(-1)=3 ≠4. Doesn't work.Next try b=1, d=-4:Equation 4: 1*(-4)=-4Equation 1: a + c=-4Equation 2:1 + (-4) + a c= -3 +a c=4 → a c=7Equation 3: a*(-4) +1*c= -4a +c=4From equation 1: c= -4 -aSubstitute into equation 3:-4a + (-4 -a)= -4a -4 -a= -5a -4=4 → -5a=8 → a= -8/5, not integer. Disregard.Next pair: b=-1, d=4.Equation 4: (-1)(4)= -4Equation 1: a +c= -4Equation 2: -1 +4 +a c=3 +a c=4 → a c=1Equation 3: a*4 + (-1)*c=4a -c=4From equation 1: c= -4 -aSubstitute into equation 3:4a - (-4 -a)=4a +4 +a=5a +4=4 →5a=0 →a=0. Then c= -4.Check equation 2: a c=0*(-4)=0≠1. Doesn't work.Next pair: b=4, d=-1.Equation 4:4*(-1)= -4Equation1: a +c= -4Equation2:4 +(-1) +a c=3 +a c=4 →a c=1Equation3: a*(-1) +4*c= -a +4c=4From equation1: c= -4 -aSubstitute into equation3:-a +4*(-4 -a)= -a -16 -4a= -5a -16=4 → -5a=20 →a= -4Then c= -4 - (-4)=0Check equation2: a c=(-4)(0)=0≠1. No good.Next pair: b=-2, d=2.Equation4: (-2)(2)= -4Equation1: a +c= -4Equation2: -2 +2 +a c=0 +a c=4 →a c=4Equation3: a*2 + (-2)*c=2a -2c=4From equation1: c= -4 -aSubstitute into equation3:2a -2*(-4 -a)=2a +8 +2a=4a +8=4 →4a= -4 →a= -1Then c= -4 -(-1)= -3Check equation2: a c= (-1)(-3)=3≠4. Doesn't work.Last pair: b=-4, d=1.Equation4: (-4)(1)= -4Equation1: a +c= -4Equation2: -4 +1 +a c= -3 +a c=4 →a c=7Equation3: a*1 + (-4)*c= a -4c=4From equation1: c= -4 -aSubstitute into equation3:a -4*(-4 -a)=a +16 +4a=5a +16=4 →5a= -12 →a= -12/5. Not integer.Thus, no factorization with integer coefficients. So maybe this quartic doesn't factor nicely. Therefore, perhaps we need to use substitution or another method.Alternatively, perhaps I made a mistake in assuming the order sin α, tan α, cos α, cot α. Maybe in reality, the AP has a different order.Alternatively, perhaps this approach is too cumbersome, and we need to consider another permutation.Wait, but in the first case, we tried the natural order when α < π/4. But maybe the actual AP is in a different order. For example, maybe the terms are arranged as sin, cos, tan, cot, but that's not ascending. Wait, in the first case, sin < tan < cos < cot. So that's the ascending order. But maybe the AP is not in ascending order? No, an arithmetic progression must be in order, either increasing or decreasing. Since all terms are positive, we can consider ascending order.Alternatively, maybe the AP skips around. For example, maybe the order is sin, cos, cot, tan or something else. But given that in α < π/4, cot is the largest, and sin is the smallest. So, if we suppose that the four terms in AP are sin, something, something, cot. Then the common difference would be (cot - sin)/3. Similarly, the middle terms would be sin + k and sin + 2k, where k = (cot - sin)/3.But maybe another approach: suppose that the four terms are in AP, so we can assign variables as follows:Let the four terms in AP be a, a + d, a + 2d, a + 3d, where a is the first term and d is the common difference. These correspond to the four trigonometric functions in some order. Therefore, we can set up equations based on this.But since we don't know the order, this might be tricky. However, considering that tan and cot are reciprocals, perhaps they are the first and last terms or the middle terms.Alternatively, note that in an AP, the sum of the first and last terms is equal to the sum of the second and third terms. So, regardless of the order, if four terms are in AP, this condition must hold. Therefore, perhaps we can consider all possible pairs of terms that could be the first and last, and see if their sum equals the sum of the remaining two terms.So, the four terms are s, c, t, k (using s = sin α, c = cos α, t = tan α, k = cot α). The possible pairs for first and last terms are:(s, c), (s, t), (s, k), (c, t), (c, k), (t, k)For each pair, check if their sum equals the sum of the other two terms.Case 1: Pair (s, c). Then, s + c should equal t + k. Let's check if this is possible.s + c = t + kSubstitute t = s/c, k = c/s:s + c = s/c + c/sMultiply both sides by sc to eliminate denominators:s^2 c + c^2 s = s^2 + c^2Factor left side:s c (s + c) = s^2 + c^2But s^2 + c^2 = 1, so:s c (s + c) = 1This seems complicated. Let me see if this is possible.Note that s and c are positive numbers less than 1, with s^2 + c^2 = 1.Let me denote x = s + c. Then, x^2 = s^2 + 2 s c + c^2 = 1 + 2 s c. Therefore, s c = (x^2 - 1)/2.So, substituting into the equation s c x = 1:(x^2 - 1)/2 * x = 1Multiply both sides by 2:x(x^2 - 1) = 2Thus:x^3 - x - 2 = 0Try to solve this cubic equation. Possible rational roots are ±1, ±2.Testing x=1: 1 -1 -2 = -2 ≠0x=2:8 -2 -2=4≠0x=-1:-1 +1 -2=-2≠0x=-2:-8 +2 -2=-8≠0So no rational roots. Using the rational root theorem, so maybe it has an irrational root. Let's try to approximate.Let f(x)=x^3 -x -2f(1)= -2f(2)=8 -2 -2=4So, by Intermediate Value Theorem, there's a root between 1 and 2.Using Newton-Raphson method:Take x0=1.5f(1.5)=3.375 -1.5 -2= -0.125f'(x)=3x² -1f'(1.5)=6.75 -1=5.75Next approximation:x1=1.5 - (-0.125)/5.75≈1.5 +0.0217≈1.5217Compute f(1.5217):(1.5217)^3 ≈1.5217*1.5217=2.3157*1.5217≈3.5243.524 -1.5217 -2≈3.524 -3.5217≈0.0023Close to zero. So root is approximately 1.5217Thus, x≈1.5217, so s + c≈1.5217But s + c can be at most sqrt(2)≈1.4142, since s^2 + c^2=1, maximum of s + c is sqrt(2) when s=c=√2/2≈0.707. But 1.5217 > sqrt(2), which is a contradiction. Therefore, no solution in this case.Thus, the pair (s, c) cannot be the first and last terms of the AP.Case 2: Pair (s, t). Check if s + t = c + ks + t = c + kSubstitute t = s/c, k = c/s:s + s/c = c + c/sMultiply both sides by sc:s^2 c + s^2 = c^2 s + c^2Rearrange terms:s^2 c - c^2 s + s^2 - c^2 =0Factor:c s (s - c) + (s^2 - c^2)=0Factor (s^2 - c^2)= (s - c)(s + c):c s (s - c) + (s - c)(s + c)=0Factor out (s - c):(s - c)(c s + s + c)=0Since α ∈ (0, π/2) and α ≠ π/4, s ≠ c. Therefore, (s - c) ≠0, so we have:c s + s + c =0But s, c >0, so c s +s + c >0. Therefore, no solution in this case.Case 3: Pair (s, k). Check if s + k = c + ts + k = c + tSubstitute k = c/s, t = s/c:s + c/s = c + s/cMultiply both sides by s c:s^2 c + c^2 = c^2 s + s^2Rearrange terms:s^2 c - c^2 s + c^2 - s^2 =0Factor:s c (s - c) + (c^2 - s^2)=0Factor (c^2 - s^2)= -(s - c)(s + c):s c (s - c) - (s - c)(s + c)=0Factor out (s - c):(s - c)(s c - (s + c))=0Again, since s ≠c, we have:s c - s - c=0Factor:s c - s - c = s(c -1) -c = 0But c = cos α <1 (since α ∈ (0, π/2)), so c -1 is negative. Therefore, s(c -1) -c = negative -c, which is negative, so cannot be zero. Therefore, no solution in this case.Case 4: Pair (c, t). Check if c + t = s + kc + t = s + kSubstitute t = s/c, k = c/s:c + s/c = s + c/sMultiply both sides by sc:c^2 s + s^2 = s^2 c + c^2Rearrange terms:c^2 s - s^2 c + s^2 - c^2 =0Factor:s c (c - s) + (s^2 - c^2)=0Factor (s^2 - c^2)= (s - c)(s + c):s c (c - s) + (s - c)(s + c)=0Factor out (s - c):(s - c)(-s c + s + c)=0Again, s ≠c, so:-s c + s + c=0 → s + c - s c=0But s + c - s c=0 → s(1 -c ) +c=0But s and c are positive, and 1 -c >0 (since c <1), so s(1 -c ) +c >0. Therefore, no solution.Case 5: Pair (c, k). Check if c +k = s +tc +k = s +tSubstitute k =c/s, t =s/c:c +c/s = s +s/cMultiply both sides by sc:c^2 s +c^2 =s^2 c +s^2Rearrange terms:c^2 s -s^2 c +c^2 -s^2=0Factor:c s (c -s ) + (c^2 -s^2)=0Factor (c^2 -s^2)= (c -s )(c +s ):c s (c -s ) + (c -s )(c +s )=0Factor out (c -s ):(c -s )(c s +c +s )=0Since c ≠s (α ≠π/4), we have:c s +c +s=0But c, s >0, so this sum is positive. No solution.Case 6: Pair (t, k). Check if t +k =s +ct +k =s +cSubstitute t =s/c, k =c/s:s/c +c/s =s +cMultiply both sides by sc:s^2 +c^2 =s c (s +c )But s^2 +c^2 =1, and s c (s +c ) is the same equation as in Case1. So, we again have 1 = s c (s +c )Which we already saw leads to x^3 -x -2=0 where x=s +c, which has no solution since s +c ≤sqrt(2)≈1.414 <1.5217. Therefore, no solution.Thus, none of the possible pairs of first and last terms satisfy the condition that their sum equals the sum of the other two terms. Therefore, there is no arithmetic progression where the four terms are s, c, t, k in any order. Therefore, the answer is no, such an angle α does not exist.Wait, but let's double-check. Maybe there's a different approach. Let's consider that in an arithmetic progression of four terms, the terms must satisfy 2b = a +c and 2c= b +d, etc. So, if we suppose that the four terms are arranged in some order, we can set up these equations.Alternatively, let's assume that the four terms are a, b, c, d in AP, so 2b = a +c and 2c = b +d.Suppose that a, b, c, d correspond to some permutation of s, c, t, k.Since there are 24 permutations, this is too many to check manually, but maybe we can find a possible permutation.Alternatively, let's consider the properties of an arithmetic progression. The average of all four terms is equal to the average of the first and last terms. So, (a + d)/2 = (a + b + c + d)/4 ⇒ 2(a + d) = a + b + c + d ⇒ a + d = b + c. Which we already considered.Alternatively, maybe consider specific values. Let's suppose that such an angle exists. Let's assume that α is such that the four terms are in AP. Let me try to suppose an angle and see.Take α=30°, which we considered earlier: sin=0.5, cos≈0.866, tan≈0.577, cot≈1.732. The terms are 0.5, 0.577, 0.866, 1.732. Let's see if any four-term AP can be formed. The differences between them are roughly 0.077, 0.289, 0.866. Not evenly spaced.Another angle, maybe α=arctan(1/2). Let's compute approximate values. tan α=0.5, so α≈26.565°. Then sin α=1/√5≈0.447, cos α=2/√5≈0.894, tan α=0.5, cot α=2. So the terms are≈0.447, 0.894, 0.5, 2. Ordering them:≈0.447, 0.5, 0.894, 2. Differences≈0.053, 0.394, 1.106. Not AP.Another angle, perhaps closer to π/4. Let's try α=35°, sin≈0.574, cos≈0.819, tan≈0.700, cot≈1.428. Ordering: 0.574, 0.700, 0.819, 1.428. Differences≈0.126, 0.119, 0.609. Not AP.Alternatively, suppose the four terms are tan α, sin α, cos α, cot α in that order. Then, check if sin α - tan α = cos α - sin α = cot α - cos α.First difference: sin - tan = cos - sin ⇒ 2 sin = tan + cos.Similarly, second difference: cos - sin = cot - cos ⇒ 2 cos = sin + cot.Let's write these equations:From first equation:2 sin α = tan α + cos αBut tan α = sin α / cos α, so:2 sin α = (sin α / cos α) + cos αMultiply both sides by cos α:2 sin α cos α = sin α + cos^2 αUsing the identity sin 2α = 2 sin α cos α:sin 2α = sin α + cos^2 αAlso, since cos^2 α = 1 - sin^2 α, substitute:sin 2α = sin α + 1 - sin^2 αRearrange:sin^2 α + sin 2α - sin α -1 =0This is a complicated equation involving sin α and sin 2α.Let me set x = sin α. Then cos α = sqrt(1 - x^2), and sin 2α = 2x sqrt(1 - x^2). Substitute into equation:x^2 + 2x sqrt(1 - x^2) -x -1 =0This looks difficult to solve analytically. Maybe try numerical methods.Let me define f(x)=x^2 +2x sqrt(1 -x^2) -x -1Looking for roots in x ∈ (0, 1). Because α ∈(0, π/2).Let's check f(0.5):f(0.5)=0.25 +2*0.5*sqrt(0.75) -0.5 -1≈0.25 +0.5*0.866 -1.5≈0.25 +0.433 -1.5≈-0.817f(0.7):f(0.7)=0.49 +2*0.7*sqrt(1 -0.49) -0.7 -1≈0.49 +1.4*sqrt(0.51)≈0.49 +1.4*0.714≈0.49 +1.0≈1.49 -0.7 -1≈-0.21f(0.8):f(0.8)=0.64 +2*0.8*sqrt(1 -0.64) -0.8 -1≈0.64 +1.6*sqrt(0.36)≈0.64 +1.6*0.6≈0.64 +0.96≈1.6 -0.8 -1≈-0.2Wait, f(0.8)≈1.6 -1.8≈-0.2. Hmm. f(0.9):f(0.9)=0.81 +2*0.9*sqrt(1 -0.81) -0.9 -1≈0.81 +1.8*sqrt(0.19)≈0.81 +1.8*0.436≈0.81 +0.785≈1.595 -1.9≈-0.305Wait, but at x=0.6:f(0.6)=0.36 +2*0.6*sqrt(1 -0.36) -0.6 -1≈0.36 +1.2*sqrt(0.64)≈0.36 +1.2*0.8≈0.36 +0.96=1.32 -1.6≈-0.28Hmm, all negative. At x=0.3:f(0.3)=0.09 +2*0.3*sqrt(0.91) -0.3 -1≈0.09 +0.6*0.954≈0.09 +0.572≈0.662 -1.3≈-0.638Wait, f(x) seems to be negative throughout. Maybe there's no solution. Let's check x=0.1:f(0.1)=0.01 +2*0.1*sqrt(0.99) -0.1 -1≈0.01 +0.2*0.995≈0.01 +0.199≈0.209 -1.1≈-0.891Still negative. x=0:f(0)=0 +0 -0 -1=-1x=1:f(1)=1 +0 -1 -1= -1So the function f(x) is always negative in (0,1). Therefore, there is no solution for this equation. Therefore, this case also doesn't work.Alternatively, maybe trying another order. Suppose the AP is sin α, cos α, cot α, tan α. Wait, but in this case, for α < π/4, the order is sin, tan, cos, cot. So this permutation would not hold. For α > π/4, the order is cos, cot, sin, tan. So maybe for α > π/4, suppose the AP is cos, cot, sin, tan. Let's check if this can be an AP.So, the four terms would be cos α, cot α, sin α, tan α. Check if the differences are equal.Difference between cot and cos: cot α - cos αDifference between sin and cot: sin α - cot αDifference between tan and sin: tan α - sin αFor it to be AP, cot α - cos α = sin α - cot α = tan α - sin αFirst, set cot α - cos α = sin α - cot αcot α - cos α = sin α - cot αBring like terms together:2 cot α = sin α + cos αExpress cot α as cos α / sin α:2 (cos α / sin α) = sin α + cos αMultiply both sides by sin α:2 cos α = sin^2 α + sin α cos αRearrange:sin^2 α + sin α cos α -2 cos α=0Factor cos α:sin^2 α + cos α (sin α -2)=0Hmm, not helpful. Let me write everything in terms of sin α. Let x = sin α, then cos α = sqrt(1 -x^2). Substitute into the equation:x^2 + sqrt(1 -x^2)(x -2)=0This seems complicated. Let me rearrange:x^2 = -sqrt(1 -x^2)(x -2)Square both sides:x^4 = (1 -x^2)(x -2)^2Expand the right side:(1 -x^2)(x^2 -4x +4)=x^2 -4x +4 -x^4 +4x^3 -4x^2Simplify:x^4 = -x^4 +4x^3 -3x^2 -4x +4Bring all terms to left:2x^4 -4x^3 +3x^2 +4x -4=0Another quartic equation. Let's check for rational roots.Possible roots: ±1, ±2, ±4, ±1/2x=1:2 -4 +3 +4 -4=1≠0x=2:32 -32 +12 +8 -4=16≠0x=1/2:2*(1/16) -4*(1/8)+3*(1/4)+4*(1/2)-4≈0.125 -0.5 +0.75 +2 -4≈-1.625≠0x=-1:2 +4 +3 -4 -4=1≠0So no rational roots. Might need to use numerical methods. Let's check approximate roots between 0 and1.Let f(x)=2x^4 -4x^3 +3x^2 +4x -4f(0.5)=2*(0.0625) -4*(0.125) +3*(0.25) +4*(0.5) -4≈0.125 -0.5 +0.75 +2 -4≈-1.625f(1)=2 -4 +3 +4 -4=1f(0.8)=2*(0.4096) -4*(0.512) +3*(0.64) +4*(0.8) -4≈0.8192 -2.048 +1.92 +3.2 -4≈-0.1088f(0.85)=2*(0.522) -4*(0.614) +3*(0.7225) +4*0.85 -4≈1.044 -2.456 +2.1675 +3.4 -4≈0.1555f(0.84)=2*(0.84)^4 -4*(0.84)^3 +3*(0.84)^2 +4*0.84 -4Calculate step by step:0.84^2=0.70560.84^3=0.84*0.7056≈0.59270.84^4≈0.84*0.5927≈0.498Thus:2*0.498≈0.996-4*0.5927≈-2.37083*0.7056≈2.11684*0.84≈3.36Sum:0.996 -2.3708≈-1.3748 +2.1168≈0.742 +3.36≈4.102 -4≈0.102So f(0.84)=≈0.102Similarly, f(0.83):0.83^2≈0.68890.83^3≈0.83*0.6889≈0.57180.83^4≈0.83*0.5718≈0.4746Thus:2*0.4746≈0.9492-4*0.5718≈-2.28723*0.6889≈2.06674*0.83≈3.32Sum:0.9492 -2.2872≈-1.338 +2.0667≈0.7287 +3.32≈4.0487 -4≈0.0487f(0.83)=≈0.0487f(0.825):0.825^2≈0.68060.825^3≈0.825*0.6806≈0.56150.825^4≈0.825*0.5615≈0.4632Thus:2*0.4632≈0.9264-4*0.5615≈-2.2463*0.6806≈2.04184*0.825=3.3Sum:0.9264 -2.246≈-1.3196 +2.0418≈0.7222 +3.3≈4.0222 -4≈0.0222f(0.825)=≈0.0222f(0.82):0.82^2≈0.67240.82^3≈0.82*0.6724≈0.55140.82^4≈0.82*0.5514≈0.4521Thus:2*0.4521≈0.9042-4*0.5514≈-2.20563*0.6724≈2.01724*0.82=3.28Sum:0.9042 -2.2056≈-1.3014 +2.0172≈0.7158 +3.28≈4.0 -4=0Approximately zero. So x≈0.82 is a root.Therefore, sin α≈0.82, so α≈arcsin(0.82)≈55 degrees.Let me check this angle, say 55 degrees.sin 55≈0.8192, cos55≈0.5736, tan55≈1.428, cot55≈0.7002So the terms are≈0.5736 (cos), 0.7002 (cot), 0.8192 (sin), 1.428 (tan). Let's check if these are in AP.Compute differences:0.7002 -0.5736≈0.12660.8192 -0.7002≈0.1191.428 -0.8192≈0.6088Not equal differences. Not an AP. Hmm, but we expected x≈0.82 to be a root. However, when we plug in x=0.82, we get sin α=0.82, then check the equation 2 cot α = sin α + cos α. Let's compute:cot α= cos α / sin α≈sqrt(1 -0.82^2)/0.82≈sqrt(1 -0.6724)=sqrt(0.3276)≈0.572/0.82≈0.6976So 2 cot α≈1.395sin α + cos α≈0.82 +0.572≈1.392Close to 1.395, which is approximately equal, considering rounding errors. So the equation is approximately satisfied, but the terms themselves don't form an AP. Therefore, even though this equation is satisfied, the other condition (next difference) may not hold.Indeed, the next condition is sin α - cot α = tan α - sin αCompute left side: sin α - cot α≈0.82 -0.6976≈0.1224Right side: tan α - sin α≈1.395 -0.82≈0.575Not equal. So, even though the first condition is approximately satisfied, the second is not. Therefore, this approach also doesn't yield a solution.Given that all possible cases have been explored and no valid solutions found, it's likely that no such angle α exists. Therefore, the answer is no.

✅:Step-by-Step Explanation and Answer:To determine if an angle (alpha in (0, pi/2)) exists such that (sin alpha), (cos alpha), (tan alpha), and (cot alpha) form an arithmetic progression (AP) in some order, we analyze the relationships and constraints between these trigonometric functions.1. Properties of Trigonometric Functions: - (sin alpha) and (cos alpha) are in ((0, 1)). - (tan alpha = frac{sin alpha}{cos alpha}) and (cot alpha = frac{1}{tan alpha}). - For (alpha in (0, pi/4)), (tan alpha < 1) and (cot alpha > 1). - For (alpha in (pi/4, pi/2)), (tan alpha > 1) and (cot alpha < 1).2. AP Conditions: - For four terms (a, b, c, d) in AP: (2b = a + c), (2c = b + d), and (a + d = b + c).3. Exploring Possible Orderings: - Considering permutations of (sin alpha), (cos alpha), (tan alpha), (cot alpha) and applying AP conditions leads to complex equations. - Key equations derived include relationships like (2 cot alpha = sin alpha + cos alpha) and others, which were checked for feasibility.4. Quartic and Cubic Equations: - Attempts to solve derived equations (e.g., (x^3 - x - 2 = 0)) show no valid roots within the required range (0 < alpha < pi/2). - Numerical methods and approximations for potential solutions (e.g., around (x approx 0.82)) fail to satisfy all AP conditions simultaneously.5. Conclusion: - All analytical and numerical approaches confirm that no such angle (alpha) exists where the four trigonometric functions form an arithmetic progression.Final Answer:(boxed{text{No}})

🔑:1. Suppose there exists an angle ( alpha in (0, pi/2) ) such that ( sin alpha, cos alpha, tan alpha, cot alpha ) taken in some order, are consecutive terms of an arithmetic progression. Let's assume ( 0 < x < frac{pi}{2} ) and ( sin x, cos x, tan x, cot x ) are in some order consecutive terms of an arithmetic progression.2. Consider the case when ( x leq frac{pi}{4} ). - We know that ( sin x leq sin frac{pi}{4} ). - Also, ( sin frac{pi}{4} = cos frac{pi}{4} ) and ( cos frac{pi}{4} leq cos x ). - Hence, we have ( sin x leq cos x < 1 ).3. Also, for ( x leq frac{pi}{4} ): - ( cot x geq 1 ), since ( cot x = frac{1}{tan x} geq 1 ) for ( x leq frac{pi}{4} ). - Since ( tan x leq 1 ) and ( sin x < tan x ). From these, we have: [ sin x leq cos x < tan x leq 1 leq cot x ] Hence, ( sin x ) is the least and ( cot x ) is the greatest among the four terms.4. Next, assume that ( sin x < cos x < tan x < cot x ) or ( sin x < tan x < cos x < cot x ). In both cases, using the property of arithmetic progression, we set: [ cos x - sin x = cot x - tan x ]5. Simplifying ( cot x - tan x ): [ cot x - tan x = frac{cos x}{sin x} - frac{sin x}{cos x} = frac{cos^2 x - sin^2 x}{cos x sin x} = frac{(cos x - sin x)(cos x + sin x)}{cos x sin x} ]6. Equating the expressions: [ cos x - sin x = frac{(cos x - sin x)(cos x + sin x)}{cos x sin x} ] - As ( cos x > sin x ), we can cancel out the common factor ( cos x - sin x ) from both sides: [ 1 = frac{cos x + sin x}{cos x sin x} ] - This simplifies to: [ 1 = frac{1}{sin x} + frac{1}{cos x} ]7. But we know: - ( 0 < sin x < 1 ) and ( 0 < cos x < 1 ), - Hence, ( frac{1}{sin x} > 1 ) and ( frac{1}{cos x} > 1 ). Thus, the sum: [ frac{1}{sin x} + frac{1}{cos x} ] is greater than 1, leading to a contradiction.8. If ( x > frac{pi}{4} ): - Consider ( pi/2 - x ), then ( 0 < frac{pi}{2} - x < frac{pi}{4} ). - The sine, cosine, tangent, and cotangent of ( frac{pi}{2} - x ) are equal to ( cos x, sin x, cot x, tan x ) respectively in some order. - Hence, the same contradiction applies. Conclusion: There does not exist an angle ( alpha in (0, pi/2) ) such that ( sin alpha, cos alpha, tan alpha, cot alpha ) are consecutive terms of an arithmetic progression. [ boxed{text{No}} ]