🧠:Okay, let's see. The problem is about coloring all natural numbers with 2017 different colors. The question is whether, no matter how you do this coloring, there must exist two numbers of the same color such that their ratio is an integer divisible by 2016. Hmm. So, the ratio of two numbers, a and b, is a/b, which is an integer and divisible by 2016. That means a/b = 2016 * k, where k is some integer. So, a = 2016 * k * b. Alternatively, since ratio is a/b, if a/b is divisible by 2016, then a must be a multiple of 2016*b. Wait, no. Let me clarify. If the ratio a/b is an integer divisible by 2016, then a/b = 2016 * m, where m is an integer. Therefore, a = 2016 * m * b. So, a has to be a multiple of 2016*b. Alternatively, if we have two numbers such that one is a multiple of the other by 2016 times some integer. But maybe we can simplify this. The problem is asking whether in any 2017-coloring of the naturals, there are two numbers of the same color where their ratio is a multiple of 2016. So, first, maybe think about the pigeonhole principle here. Since we have 2017 colors, if we can find a structure in the natural numbers that requires more than 2017 elements, such that within that structure, any two elements have a ratio divisible by 2016, then by the pigeonhole principle, two elements must share the same color. Wait, but the ratio being divisible by 2016 is a specific condition. Let me think again. If we can create an infinite set of numbers where each number is a multiple of the previous one by 2016, then any two numbers in this set would have a ratio that is a multiple of 2016. But how?Alternatively, maybe think in terms of residues or equivalence classes. Let's consider numbers modulo something. Wait, 2016 factors into prime factors. Let's factorize 2016. 2016 = 2^5 * 3^2 * 7^1. So, prime factors 2, 3, 7 with exponents 5, 2, 1. Now, maybe we can construct numbers in such a way that their ratios would cover these prime factors. Hmm. Alternatively, perhaps use the Chinese Remainder Theorem or van der Waerden's theorem? Wait, but van der Waerden is about arithmetic progressions. Maybe not directly applicable.Alternatively, consider building a sequence of numbers where each is 2016 times the previous one. For example, starting with 1, then 2016, then 2016^2, 2016^3, etc. Then, the ratio between any two numbers in this sequence where the later term is divided by an earlier term is 2016^(k), which is a multiple of 2016. So, if we have such a geometric progression, then any two numbers in the sequence have a ratio that is a multiple of 2016. If we can show that such a sequence must have two numbers of the same color, then we are done. Since there are 2017 colors, if the sequence has 2018 numbers, then by pigeonhole principle, two of them must share the same color. Therefore, if we take the numbers 2016^0, 2016^1, ..., 2016^{2017}, which is 2018 numbers, then two of them must have the same color. The ratio between any two of these is 2016^{k - m}, which for k > m, is 2016^{k - m}, which is divisible by 2016. So, that seems like a valid approach. Therefore, the answer is yes, it's always true. Wait, but hold on. The problem states "their ratio is an integer and divisible by 2016." So, if you take two numbers from the sequence, say 2016^k and 2016^m where k > m, then their ratio is 2016^{k - m}, which is an integer and divisible by 2016. So that's exactly what we need. Therefore, by constructing such a sequence of length 2018, which requires only 2017 colors, we force two numbers in the sequence to share a color, and their ratio is divisible by 2016. Therefore, the answer is yes.But wait, let me check. The numbers in the sequence are 1, 2016, 2016^2, ..., 2016^{2017}. There are 2018 numbers here. So, by the pigeonhole principle, with 2017 colors, two must be the same color. Their ratio is a power of 2016, hence divisible by 2016. Therefore, regardless of how the coloring is done, such a pair must exist. Therefore, the answer should be yes, it's true.But maybe I made a mistake here. Let me think again. Suppose we color each number in the sequence 2016^k with a different color. Wait, but the problem allows coloring all natural numbers in 2017 colors, but the sequence has 2018 numbers, so even if the coloring is arbitrary, two numbers in the sequence must share the same color. Hence, regardless of the coloring method, such a pair exists. Therefore, the answer is yes. Therefore, the statement is true.Alternatively, is there a way to color the numbers such that no two numbers in the geometric progression share the same color? But since we have only 2017 colors and 2018 numbers in the sequence, you can't color all of them with distinct colors. Therefore, no matter how you color them, two numbers in the sequence must share the same color. Therefore, the pair exists. Therefore, the answer is yes. So, regardless of the coloring, you can always find such a pair. Therefore, the statement is true.But wait, the problem says "their ratio is an integer and divisible by 2016". So, the ratio must be an integer, which it is, since it's 2016^{k - m}, and divisible by 2016, which is true as long as k - m >= 1. Therefore, any two numbers in the sequence where the exponent differs by at least 1 will satisfy the condition. Therefore, if two numbers in the sequence share the same color, their ratio is 2016^{difference}, which is divisible by 2016. Therefore, the conclusion holds. Therefore, the answer is yes. So, the answer should be boxed{Yes} or in the required format, probably boxed{Yes} in Chinese or as per instruction. Wait, the user didn't specify Chinese. The original problem is in English, so the answer is boxed{Yes}. But wait, to make sure, let's check for possible oversights. For example, what if the coloring is done in a way that all numbers in the geometric progression are colored with different colors, but since there are 2018 numbers and 2017 colors, that's impossible. So, at least two must share the same color. Therefore, such a pair must exist. Hence, the answer is yes. Therefore, the statement is true.Final Answerboxed{Yes}

✅:To determine whether it is always true that regardless of the way of coloring all natural numbers with 2017 different colors, one can always find two numbers of the same color such that their ratio is an integer and divisible by 2016, we can use the pigeonhole principle and construct a specific sequence of numbers.1. Prime Factorization of 2016: [ 2016 = 2^5 times 3^2 times 7 ] This factorization helps in understanding the structure of numbers divisible by 2016.2. Constructing a Geometric Progression: Consider the sequence of numbers formed by powers of 2016: [ 1, 2016, 2016^2, 2016^3, ldots, 2016^{2017} ] This sequence has 2018 numbers. The ratio between any two numbers in this sequence (where the exponent of the later term is greater) is (2016^{k - m}), which is an integer and divisible by 2016.3. Applying the Pigeonhole Principle: Since there are 2017 colors and 2018 numbers in the sequence, by the pigeonhole principle, at least two numbers in this sequence must be colored the same. The ratio of these two numbers is a power of 2016, hence divisible by 2016.Thus, regardless of the coloring method, there will always be two numbers in the sequence with the same color whose ratio is an integer divisible by 2016. Therefore, the answer is:[boxed{Yes}]

🔑:1. Let's consider the set of natural numbers (1, 2016, 2016^2, ldots, 2016^{2017}).2. This set contains (2018) numbers.3. According to the problem, there are (2017) different colors available to paint these numbers.4. By the pigeonhole principle (since we have more numbers than colors), at least two numbers among (1, 2016, 2016^2, ldots, 2016^{2017}) must be painted the same color.5. Suppose (2016^a) and (2016^b) are two such numbers, where (a) and (b) are integers such that (0 leq a < b leq 2017), sharing the same color.6. The ratio of these two numbers is ( frac{2016^b}{2016^a} = 2016^{b-a} ).7. Since (b-a) is a positive integer, the ratio (2016^{b-a}) is a whole number.8. Furthermore, (2016^{b-a}) is clearly divisible by (2016).Therefore, we conclude that it is indeed true that for any coloring of the natural numbers using (2017) colors, there must exist at least two numbers of the same color such that one is divisible by the other and the ratio is an integer multiple of (2016).(boxed{text{True}})

🧠:Okay, let's tackle this problem about a geometric sequence. So, we're given that in a geometric sequence {a_n}, all terms are positive. The equation provided is 2a₄ + a₃ - 2a₂ - a₁ = 8. We need to find the minimum value of 2a₈ + a₇. Hmm, let's start by recalling what a geometric sequence is. In a geometric sequence, each term after the first is found by multiplying the previous term by a constant called the common ratio, usually denoted as r. So, if the first term is a₁, then a₂ = a₁ * r, a₃ = a₁ * r², and so on. In general, aₙ = a₁ * r^(n-1). That's the formula I need to use here.Given that all terms are positive, both a₁ and r must be positive numbers. Since the problem mentions finding the minimum value, I suspect calculus might come into play here, maybe taking derivatives to find minima. But first, let me express all the terms in the given equation in terms of a₁ and r.So, let's rewrite the given equation: 2a₄ + a₃ - 2a₂ - a₁ = 8.Substituting each term with the formula for a geometric sequence:2(a₁ * r³) + (a₁ * r²) - 2(a₁ * r) - a₁ = 8.Let me factor out a₁ from each term:a₁ [2r³ + r² - 2r - 1] = 8.So, we have a₁ multiplied by some expression involving r equals 8. Our goal is to find the minimum of 2a₈ + a₇. Let's express a₈ and a₇ in terms of a₁ and r as well.a₇ = a₁ * r⁶a₈ = a₁ * r⁷Therefore, 2a₈ + a₇ = 2(a₁ * r⁷) + a₁ * r⁶ = a₁ * r⁶ (2r + 1).So, 2a₈ + a₇ = a₁ * r⁶ (2r + 1). Our task is to minimize this expression. However, a₁ is related to r through the equation a₁ [2r³ + r² - 2r - 1] = 8. Therefore, we can express a₁ in terms of r:a₁ = 8 / [2r³ + r² - 2r - 1].Therefore, substituting back into the expression we need to minimize:2a₈ + a₇ = [8 / (2r³ + r² - 2r - 1)] * r⁶ (2r + 1).Simplify this expression:Let me write that as 8 * r⁶ (2r + 1) / (2r³ + r² - 2r - 1).So, the problem reduces to minimizing the function f(r) = [8 r⁶ (2r + 1)] / [2r³ + r² - 2r - 1] where r > 0 (since all terms are positive), and also the denominator must not be zero. Also, since all terms in the sequence are positive, the denominator 2r³ + r² - 2r - 1 must be positive as well. Otherwise, a₁ would be negative, which contradicts the given condition. So, 2r³ + r² - 2r - 1 > 0.Therefore, we need to find r > 0 such that 2r³ + r² - 2r - 1 > 0 and minimize f(r).First, let's figure out the domain of r. Let's find where 2r³ + r² - 2r - 1 = 0. Maybe factor this cubic equation.Trying rational roots. The possible rational roots are ±1, ±1/2.Testing r = 1: 2(1)³ + (1)² - 2(1) - 1 = 2 + 1 - 2 - 1 = 0. So, r = 1 is a root. Therefore, we can factor (r - 1) out of the cubic.Using polynomial division or synthetic division to factor.Dividing 2r³ + r² - 2r - 1 by (r - 1):Using synthetic division:Coefficients: 2 | 1 | -2 | -1Root at r = 1:Bring down the 2.Multiply 2 by 1 = 2. Add to next coefficient: 1 + 2 = 3.Multiply 3 by 1 = 3. Add to next coefficient: -2 + 3 = 1.Multiply 1 by 1 = 1. Add to last coefficient: -1 + 1 = 0.So, the cubic factors as (r - 1)(2r² + 3r + 1).Now, factor the quadratic: 2r² + 3r + 1. Let's see, discriminant is 9 - 8 = 1. So, roots at (-3 ±1)/4. So, (-3 +1)/4 = -0.5, (-3 -1)/4 = -1. Therefore, factors as (2r + 1)(r + 1).Therefore, the cubic factors as (r - 1)(2r + 1)(r + 1).Therefore, the denominator is 2r³ + r² - 2r -1 = (r - 1)(2r + 1)(r + 1).Therefore, the denominator is positive when (r - 1)(2r + 1)(r + 1) > 0.Since r > 0, and all terms are positive, we need to consider r > 0, but (r + 1) is always positive, 2r + 1 is always positive for r > 0. Therefore, the sign of the denominator is determined by (r - 1). Therefore, denominator is positive when r -1 > 0, i.e., r > 1. If r < 1, then denominator is negative. However, since all terms in the sequence are positive, denominator must be positive, so r must be greater than 1.Wait, let's confirm that. The denominator is (r - 1)(2r + 1)(r + 1). Since r > 0, (2r + 1) > 0 and (r + 1) > 0. Therefore, the denominator's sign is the same as (r - 1). So, denominator is positive when r > 1, negative when r < 1. But since a₁ = 8 / denominator, and a₁ must be positive, denominator must be positive. Therefore, r > 1. So, our domain is r > 1.Therefore, r must be greater than 1. So, we need to minimize f(r) = [8 r⁶ (2r + 1)] / [(r - 1)(2r + 1)(r + 1)] for r > 1.Wait, but notice that (2r + 1) appears in both numerator and denominator. Let's see:Wait, the denominator was (r - 1)(2r + 1)(r + 1). The numerator is 8 r⁶ (2r + 1). Therefore, we can cancel (2r + 1) from numerator and denominator, provided 2r +1 ≠0. But since r >1, 2r +1 is positive, so it's okay. Therefore, simplifying f(r):f(r) = [8 r⁶ (2r + 1)] / [(r - 1)(2r + 1)(r + 1)] = [8 r⁶] / [(r - 1)(r + 1)].Simplify denominator: (r -1)(r +1) = r² -1. Therefore, f(r) = 8 r⁶ / (r² -1).Therefore, the problem reduces to minimizing f(r) = 8 r⁶ / (r² -1) for r > 1.So, now we need to find the minimum of f(r) = 8r⁶ / (r² -1) where r >1. Let's focus on this function.To find the minimum, take the derivative f’(r) and set it to zero.First, let's compute f’(r). Let me write f(r) as 8 * r⁶ / (r² - 1). Let’s denote f(r) = 8 * [r⁶ / (r² - 1)]. So, f’(r) = 8 * [ ( (6r⁵)(r² -1) - r⁶(2r) ) / (r² -1)² ]Compute numerator:6r⁵(r² -1) - r⁶(2r) = 6r⁷ -6r⁵ -2r⁷ = (6r⁷ -2r⁷) -6r⁵ = 4r⁷ -6r⁵.Factor out 2r⁵:2r⁵(2r² -3).Therefore, f’(r) = 8 * [ 2r⁵(2r² -3) / (r² -1)² ]Set derivative equal to zero. The denominator is always positive for r >1, so critical points occur when numerator is zero. So, 2r⁵(2r² -3) =0. Since r >1, 2r⁵ is never zero. Therefore, 2r² -3 =0 => r² = 3/2 => r = sqrt(3/2) = sqrt(6)/2 ≈1.2247.Therefore, critical point at r = sqrt(6)/2. Now, we need to check if this is a minimum.We can perform the second derivative test or analyze the sign of the first derivative around r = sqrt(6)/2.Let’s check the sign of f’(r):For r > sqrt(6)/2, say r = 2, then 2r² -3 = 8 -3=5>0, so f’(r) positive.For r between 1 and sqrt(6)/2, say r=1.1, then 2*(1.21) -3 =2.42-3= -0.58 <0, so f’(r) negative.Therefore, the function f(r) decreases on (1, sqrt(6)/2) and increases on (sqrt(6)/2, ∞). Therefore, r = sqrt(6)/2 is the point of minima.Therefore, the minimum value is f(sqrt(6)/2). Let's compute this.First, compute r = sqrt(6)/2. Let's compute r²: (sqrt(6)/2)² = 6/4 = 3/2.So, r² = 3/2. Then, r⁶ = (r²)^3 = (3/2)^3 =27/8.Also, r² -1 =3/2 -1 =1/2.Therefore, f(r)=8 * r⁶/(r² -1)=8*(27/8)/(1/2)= (27)/(1/2)=54.Wait, let's check that step by step.Wait, f(r)=8 * [r⁶/(r² -1)]r⁶/(r² -1) = (27/8) / (1/2) )= (27/8)*(2/1)=54/8=27/4.Then, 8*(27/4)= 27*2=54. Yes, correct.Therefore, the minimum value is 54. Therefore, the minimum value of 2a₈ +a₇ is 54.But let me verify this step by step to make sure.Given that r= sqrt(6)/2. Let's compute a₁.From the original equation: a₁ =8 / [2r³ + r² -2r -1].But earlier, we had 2r³ + r² -2r -1= (r -1)(2r +1)(r +1). But since r= sqrt(6)/2 ≈1.2247, which is greater than 1, so denominator is positive.Alternatively, compute denominator:2r³ + r² -2r -1. Let's compute each term:r = sqrt(6)/2 ≈1.2247r² = 6/4 =3/2=1.5r³ = r² * r =1.5 * sqrt(6)/2 = (3/2)*(sqrt(6)/2)= (3 sqrt(6))/4≈ (3*2.449)/4≈7.347/4≈1.8368Therefore, 2r³=2*1.8368≈3.6736r²=1.5-2r≈-2*1.2247≈-2.4494-1= -1So sum up: 3.6736 +1.5 -2.4494 -1≈3.6736+1.5=5.1736; 5.1736 -2.4494=2.7242; 2.7242 -1=1.7242. So denominator≈1.7242. Therefore, a₁=8 /1.7242≈4.64.Then, 2a₈ +a₇= a₁ * r⁶(2r +1). Let's compute each part.a₁≈4.64r= sqrt(6)/2≈1.2247r⁶= (sqrt(6)/2)^6. Let's compute that. Since r²=3/2, then r⁶=(r²)^3=(3/2)^3=27/8=3.375.2r +1=2*(sqrt(6)/2)+1= sqrt(6)+1≈2.449+1≈3.449.Therefore, 2a₈ +a₇≈4.64 *3.375 *3.449. Let's compute that step by step.First, 4.64*3.375≈4.64*3 +4.64*0.375≈13.92 +1.74≈15.66.Then, 15.66*3.449≈15*3.449 +0.66*3.449≈51.735 +2.276≈54.011. So approximately 54.011, which is about 54. So, matches the earlier calculation.Therefore, the minimum value is 54. Hence, the answer is 54. Let me check if this is correct through another approach.Alternatively, since the problem is about minimizing 2a₈ +a₇, given the constraint 2a₄ +a₃ -2a₂ -a₁=8. Perhaps we can use substitution with variables.Let me think: Let’s denote r as the common ratio. Then, express all terms in terms of a₁ and r, as done before, leading to the expression in terms of r, which is 8r⁶/(r² -1). Then, by taking derivative, we found minimum at r= sqrt(6)/2, giving 54. That seems consistent.Alternatively, maybe using substitution variables. Let’s set t = r². Since r >1, t >1.Then, note that f(r)=8r⁶/(r² -1)=8t³/(t -1). Let’s define g(t)=8t³/(t -1) where t >1. Find the minimum of g(t). Take derivative:g’(t)=8[3t²(t -1) - t³(1)]/(t -1)²=8[3t³ -3t² -t³]/(t -1)²=8[2t³ -3t²]/(t -1)²=8t²(2t -3)/(t -1)².Set derivative to zero: numerator=0 =>8t²(2t -3)=0. Since t>1, t²≠0, so 2t -3=0 => t=3/2.Therefore, critical point at t=3/2. Since for t>3/2, g’(t) positive, and for 1 < t <3/2, g’(t) negative, so t=3/2 is the minimum. Therefore, minimum value is g(3/2)=8*( (3/2)^3 )/( (3/2)-1 )=8*(27/8)/(1/2)=27/(1/2)=54. Same result. So, confirms that the minimum is indeed 54.Therefore, after thorough analysis and multiple approaches, the minimum value is 54.Final Answerboxed{54}

✅:Given a geometric sequence ({a_n}) with all terms positive, we know that (2a_4 + a_3 - 2a_2 - a_1 = 8). We need to find the minimum value of (2a_8 + a_7).First, express the terms of the geometric sequence in terms of the first term (a_1) and the common ratio (r):[a_1 = a_1, quad a_2 = a_1 r, quad a_3 = a_1 r^2, quad a_4 = a_1 r^3]Substituting these into the given equation:[2a_4 + a_3 - 2a_2 - a_1 = 8 implies 2a_1 r^3 + a_1 r^2 - 2a_1 r - a_1 = 8]Factoring out (a_1):[a_1 (2r^3 + r^2 - 2r - 1) = 8 implies a_1 = frac{8}{2r^3 + r^2 - 2r - 1}]Next, express (2a_8 + a_7) in terms of (a_1) and (r):[2a_8 + a_7 = 2a_1 r^7 + a_1 r^6 = a_1 r^6 (2r + 1)]Substituting (a_1) from the earlier equation:[2a_8 + a_7 = frac{8}{2r^3 + r^2 - 2r - 1} cdot r^6 (2r + 1)]Simplify the expression:[2a_8 + a_7 = frac{8r^6 (2r + 1)}{2r^3 + r^2 - 2r - 1}]Factor the denominator:[2r^3 + r^2 - 2r - 1 = (r - 1)(2r + 1)(r + 1)]Since all terms are positive, (r > 1). Simplifying further:[2a_8 + a_7 = frac{8r^6 (2r + 1)}{(r - 1)(2r + 1)(r + 1)} = frac{8r^6}{(r - 1)(r + 1)} = frac{8r^6}{r^2 - 1}]To minimize (frac{8r^6}{r^2 - 1}) for (r > 1), take the derivative and set it to zero:[f(r) = frac{8r^6}{r^2 - 1}, quad f'(r) = frac{8 cdot 2r^5(2r^2 - 3)}{(r^2 - 1)^2}]Setting the numerator to zero:[2r^5(2r^2 - 3) = 0 implies 2r^2 - 3 = 0 implies r^2 = frac{3}{2} implies r = sqrt{frac{3}{2}} = frac{sqrt{6}}{2}]Substitute (r = frac{sqrt{6}}{2}) back into the expression:[r^2 = frac{3}{2}, quad r^6 = left(frac{3}{2}right)^3 = frac{27}{8}, quad r^2 - 1 = frac{1}{2}][frac{8r^6}{r^2 - 1} = frac{8 cdot frac{27}{8}}{frac{1}{2}} = frac{27}{frac{1}{2}} = 54]Thus, the minimum value of (2a_8 + a_7) is (boxed{54}).

🔑:1. We start by defining the geometric sequence {a_n} with a common ratio q, where q > 0.2. Given the condition: [ 2a_4 + a_3 - 2a_2 - a_1 = 8 ]3. Express each term in the sequence using the first term a_1 and the common ratio q: [ a_2 = a_1 q, quad a_3 = a_1 q^2, quad a_4 = a_1 q^3 ]4. Substitute these expressions into the given equation: [ 2a_1 q^3 + a_1 q^2 - 2a_1 q - a_1 = 8 ]5. Factor out a_1: [ a_1 (2q^3 + q^2 - 2q - 1) = 8 ]6. Simplify the equation to isolate the common ratio terms: [ 2a_1 q^3 + a_1 q^2 - 2a_1 q - a_1 = 8 implies a_1 (2q^3 + q^2 - 2q - 1) = 8 ]7. Let t = q^2 - 1, hence q^2 = t + 1, and since q > 1, we have t > 0.8. We need to find the expression for 2a_8 + a_7. Substitute the terms in geometric sequence: [ 2a_8 + a_7 = 2a_1 q^7 + a_1 q^6 ]9. Factor out a_1: [ 2a_1 q^7 + a_1 q^6 = a_1(2q^7 + q^6) ]10. Using the earlier found relationship a_1 (2q^3 + q^2 - 2q - 1) = 8: [ 2a_1 q^3 + a_1 q^2 - 2a_1 q - a_1 = 8 implies a_1 (2q^3 + q^2 - 2q - 1) = 8 ] Solve for a_1: [ a_1 = frac{8}{2q^3 + q^2 - 2q - 1} ]11. Substitute back into the expression for 2a_8 + a_7: [ 2a_8 + a_7 = frac{8}{2q^3 + q^2 - 2q - 1} (2q^7 + q^6) ]12. Simplify the expression with t: [ 2a_8 + a_7 = frac{8(2q^7 + q^6)}{2q^3 + q^2 - 2q - 1} ]13. Using q^2 = t+1: [ q^6 = (t + 1)^3 quad text{and} quad q^7 = q(t + 1)^3 ]14. Thus, [ 2q^7 + q^6 = 2 q(t+1)^3 + (t+1)^3 = (2q + 1)(t+1)^3 ]15. Therefore: [ 2a_8 + a_7 = frac{8(2q + 1)(t + 1)^3}{2q^3 + q^2 - 2q - 1} = frac{8(t+1)^3}{t} ]16. Simplify further: [ frac{8(t+1)^3}{t} = 8 left( t + 3 + 3 + frac{1}{t} right) ]17. Take the function f(t) = 8(t^2 + 3t + 3 + frac{1}{t}) and find its derivative: [ f'(t) = 8 left(2t + 3 - frac{1}{t^2} right) ]18. Analyze the function to find its turning points and determine: [ f'(t) = 8 left( frac{2t^3 + 3t^2 - 1}{t^2} right) = 8 left( frac{(t+1)^2(2t-1)}{t^2} right) ]19. Determine the minimum value occurs at t = frac{1}{2}: [ fleft( frac{1}{2} right) = 8 left( left(frac{1}{2}right)^2 + 3(frac{1}{2}) + 3 + frac{2}{1} right) = 54 ]20. Therefore, the minimum value: [ boxed{54} ]

🧠:Okay, so I have this inequality to solve: (log _{a}left(a-frac{x^{2}}{2}right)>log _{a}(a-x)). The solution set is called A, and when we take the intersection of A with the integers, we get just {1}. I need to find the range of values for a. Hmm, let's start by recalling some properties of logarithmic functions.First, logarithms are only defined when their arguments are positive. So, for both (log _{a}left(a-frac{x^{2}}{2}right)) and (log _{a}(a-x)) to be valid, the arguments inside must be greater than 0. That gives me two conditions:1. (a - frac{x^2}{2} > 0)2. (a - x > 0)Also, the base a of the logarithm must satisfy (a > 0) and (a neq 1).Next, the inequality (log _{a}left(a-frac{x^{2}}{2}right)>log _{a}(a-x)) can be simplified by considering the properties of logarithmic functions. If the base a is greater than 1, then the logarithm is increasing, so the inequality between the arguments is preserved. If the base is between 0 and 1, the logarithm is decreasing, so the inequality between the arguments is reversed.Therefore, I need to split this problem into two cases:Case 1: (a > 1)In this case, since the logarithm is increasing, the inequality (log _{a}left(a-frac{x^{2}}{2}right)>log _{a}(a-x)) implies:(a - frac{x^2}{2} > a - x)Simplifying this:Subtract a from both sides: (-frac{x^2}{2} > -x)Multiply both sides by -2 (remember to reverse the inequality):(x^2 < 2x)Bring all terms to one side:(x^2 - 2x < 0)Factor:(x(x - 2) < 0)This inequality holds when x is between 0 and 2. So, the solution here is (0 < x < 2). But we also need to consider the domain where the original logarithms are defined.From the domain conditions:1. (a - frac{x^2}{2} > 0) → (x^2 < 2a) → (-sqrt{2a} < x < sqrt{2a})2. (a - x > 0) → (x < a)So, combining all the conditions for Case 1:- (0 < x < 2) (from the inequality)- (x < a) (from the domain of the second logarithm)- (-sqrt{2a} < x < sqrt{2a}) (from the domain of the first logarithm)But since the inequality solution is (0 < x < 2), we can focus on this interval. We need to ensure that (0 < x < 2) is within the domain. Since (x < a) must hold for all x in (0,2), the upper bound here is 2, so a must be greater than 2 to satisfy x < a for all x up to 2. Wait, but if a is greater than 2, then x < a is automatically true for x in (0,2). Also, (x^2 < 2a) for x in (0,2). The maximum x^2 in this interval is 4 (when x=2), but since x is less than 2, the maximum x^2 is approaching 4. So 2a must be greater than 4, which means a > 2. Wait, but hold on, if x approaches 2, then x^2 approaches 4, so we need 2a > 4 → a > 2. So combining these, for Case 1 (a > 1), the domain constraints require a > 2. Then the solution set A is (0,2). However, the problem states that A ∩ Z = {1}. But if A is (0,2), then the integers in A are {1}, which matches the given condition. Wait, but in this case, if a > 2, then the solution set is (0,2), which when intersected with integers gives {1}, which is exactly what the problem states. So for Case 1, a > 2 would work? But let's check.Wait, hold on. If a is greater than 2, then the domain for x is x < a and x^2 < 2a. Since a > 2, x < a is automatically true for x < 2. Also, x^2 < 2a: since x is less than 2, x^2 is less than 4, and 2a is greater than 4 (since a > 2), so x^2 < 4 < 2a. So the domain is satisfied. Therefore, the solution set is (0,2). The integers in this interval are just 1. So that seems okay. But let's check another case.Case 2: (0 < a < 1)Here, the logarithm is decreasing, so the inequality reverses when we remove the logs. So:(a - frac{x^2}{2} < a - x)Simplify:Subtract a from both sides: (-frac{x^2}{2} < -x)Multiply both sides by -2 (reverse inequality again):(x^2 > 2x)Bring all terms to one side:(x^2 - 2x > 0)Factor:(x(x - 2) > 0)So, this inequality holds when x < 0 or x > 2. However, we need to consider the domain where the original logarithms are defined.Domain conditions:1. (a - frac{x^2}{2} > 0) → (x^2 < 2a) → (-sqrt{2a} < x < sqrt{2a})2. (a - x > 0) → (x < a)Now, since 0 < a < 1, the domain for x is x < a and x must be between (-sqrt{2a}) and (sqrt{2a}). But since a is between 0 and 1, (sqrt{2a}) is between 0 and (sqrt{2}) (~1.414). Also, x must be less than a, which is less than 1. So the domain for x is x < a, and x must be greater than (-sqrt{2a}). However, the solution from the inequality is x < 0 or x > 2. But since in the domain x < a < 1, the x > 2 part is impossible. So only x < 0 is part of the solution. But x must also be greater than (-sqrt{2a}). So the solution set here is (-sqrt{2a} < x < 0). However, we need to check if this interval contains any integers. The integers in (-sqrt{2a} < x < 0) would be x = -1, -2, etc., but since a is between 0 and 1, (sqrt{2a}) is less than sqrt(2) ≈ 1.414. So (-sqrt{2a}) is greater than -1.414. Therefore, x must be greater than -1.414 and less than 0. The integers in this interval would be x = -1. But since the problem states that A ∩ Z = {1}, which does not include -1. Therefore, in this case, if there are integer solutions, they would include -1, which contradicts the given condition. Therefore, Case 2 (0 < a < 1) is impossible, because it would result in A ∩ Z containing -1, which is not allowed. Therefore, only Case 1 (a > 1) is possible.But wait, in Case 1, we concluded that a > 2 would give solution set (0,2) with A ∩ Z = {1}. But the problem says that A ∩ Z = {1}. However, maybe there are other constraints. Let's check again.Wait, if a is exactly 2, then in Case 1 (a > 1), then the domain conditions:1. (x^2 < 2a = 4), so x ∈ (-2,2)2. (x < a = 2)So combined with the inequality solution (0,2). Therefore, if a = 2, the solution set is still (0,2), which gives A ∩ Z = {1}. So a = 2 is also acceptable.Wait, but earlier in Case 1, we considered a > 2. Let me check if a = 2 is allowed. When a = 2, the original logarithms:For (log_{2}(2 - x^2/2)) and (log_{2}(2 - x)). The arguments must be positive. So 2 - x^2/2 > 0 → x^2 < 4 → x ∈ (-2,2). And 2 - x > 0 → x < 2. So the domain is x ∈ (-2,2). The inequality solution is (0,2). So integers in (0,2) are {1}. So a = 2 is acceptable.But earlier, when I considered a > 2, the domain is x < a and x ∈ (-sqrt(2a), sqrt(2a)). Since a > 2, sqrt(2a) > sqrt(4) = 2, so the upper bound is sqrt(2a) > 2, but since x < a, and a > 2, the domain for x is (-sqrt(2a), a). But since the inequality solution is (0,2), which is within (-sqrt(2a), a) as long as a > 2. So even if a is greater than 2, the solution set is still (0,2). Therefore, for all a >= 2, the solution set A is (0,2), hence A ∩ Z = {1}. Wait, but the problem says that A ∩ Z = {1}. So if a is greater than 2, then the solution set is (0,2), but when a is exactly 2, the solution set is still (0,2). So the range for a is a >= 2?Wait, but let me check when a is between 1 and 2. Suppose a is 1.5. Then in Case 1 (a > 1), the inequality solution is (0,2). But we have to check the domain:1. (a - x^2/2 > 0) → x^2 < 2a = 3. So x ∈ (-sqrt(3), sqrt(3)) ≈ (-1.732, 1.732)2. (a - x > 0) → x < 1.5So the domain for x is (-sqrt(3), 1.5). But the inequality solution is (0,2). The overlap between (0,2) and (-sqrt(3),1.5) is (0,1.5). Therefore, the actual solution set A is (0,1.5). Then, A ∩ Z would be {1}, since 1.5 is not an integer, and the interval is (0,1.5). So integers are {1}. Wait, so even if a is between 1 and 2, the solution set A is (0, a), and A ∩ Z is {1} only if a is between 1 and 2? Wait, let me check:If a is 1.5, then A is (0,1.5). So integers in A are {1}. If a is 1.2, then A is (0,1.2), integers in A are still {1}. If a is 1.9, then A is (0,1.9), integers in A are {1}. So actually, if a is in (1,2), then A is (0,a). But when a is in (1,2), the domain from (x^2 < 2a) is x ∈ (-sqrt(2a), sqrt(2a)). Since sqrt(2a) when a is between 1 and 2 is sqrt(2) to 2. So sqrt(2a) is approximately 1.414 to 2. So the domain for x is (-sqrt(2a), a). Since a is between 1 and 2, sqrt(2a) is between sqrt(2) ≈1.414 and 2. So the upper bound for x is a, which is less than 2. Therefore, the domain is x ∈ (-sqrt(2a), a). The inequality solution is (0,2). Therefore, the overlap between (0,2) and (-sqrt(2a), a) is (0, a). Therefore, the actual solution set A is (0, a). Then, A ∩ Z would be {1} only if a is between 1 and 2. Because if a is between 1 and 2, then (0,a) includes 1 only if a >1. If a is exactly 1, then (0,1) doesn't include 1. But the problem says A ∩ Z = {1}. So if a is in (1,2), then A is (0,a), and since a < 2, the integers in (0,a) are only 1 if a is between 1 and 2. For example, if a is 1.5, integers in (0,1.5) are {1}. If a is 1.9, same. If a is 2, then A is (0,2), which still only includes {1} in integers. If a is greater than 2, then A is (0,2), because the inequality solution is (0,2) but the domain allows up to 2, but since in the domain x < a, and a > 2, the upper limit is still 2. Wait, no, if a is greater than 2, the domain is x < a and x ∈ (-sqrt(2a), sqrt(2a)). Since sqrt(2a) is greater than 2, but the inequality solution is (0,2). Therefore, even if a > 2, the solution set remains (0,2), so A ∩ Z = {1}. Therefore, if a is greater than or equal to 2, the solution set is (0,2), integers {1}. If a is between 1 and 2, the solution set is (0,a), which still only includes integer 1. Wait, but in that case, the answer would be a > 1. But wait, when a is between 1 and 2, the solution set is (0,a), so if a is between 1 and 2, then (0,a) includes 1 only if a >1, which it is. But the integer 1 is included as long as a >1, because 1 is in (0,a) when a >1. But if a is exactly 1, the log base is 1, which is invalid. So the base a must be greater than 1. Therefore, combining both cases, when a >1, but we need to check for different intervals.Wait, but earlier when a is between 1 and 2, the solution set is (0,a), and when a >=2, it's (0,2). In both cases, the integer solution is {1}, so perhaps the range of a is (1, ∞). But wait, no, because when a is between 1 and 2, the solution set is (0,a), which includes 1 if a >1, but if a approaches 1 from the right, say a =1.1, then the solution set is (0,1.1), which still contains 1. So in that case, the integers in A are {1}. Similarly, if a is 3, the solution set is (0,2), integers {1}. So actually, all a >1 would result in A ∩ Z = {1}. But wait, this contradicts earlier analysis where if a is between 1 and 2, the solution set is (0,a), but when a is greater than 2, it's (0,2). But in both cases, the only integer in A is 1. Therefore, the range of a is a >1. But the problem says "the set of solutions to the inequality is A, and A ∩ Z = {1}". Therefore, the answer should be a >1. But this seems conflicting with earlier steps.Wait, but let's test with a=1.5. If a=1.5, then the solution set is (0,1.5). The integer in this interval is 1. So A ∩ Z = {1}, which is correct. If a=2, solution set (0,2), integers {1}. If a=3, solution set (0,2), same. If a=1.5, solution set (0,1.5). All these satisfy A ∩ Z = {1}. But wait, what if a=1.0? If a=1, the base is invalid. So a must be greater than 1. Therefore, the answer seems to be a >1. But earlier when we considered Case 1 (a >1), we split into a >2 and 1 <a <2. However, regardless of whether a is between 1 and 2 or greater than 2, the integer solutions are {1}. So why was there confusion earlier? Because I thought when a is between 1 and 2, the solution set is (0,a), but in reality, when a is between 1 and 2, the inequality solution is (0,2), but the domain restricts it to (0,a). However, when a is between 1 and 2, the original inequality's solution is (0,2), but due to domain constraints, x must be less than a. Therefore, the actual solution set is (0, a). Hence, A = (0, a) when 1 <a <2, and A = (0,2) when a >=2. Both cases give A ∩ Z = {1}, since in the first case, a <2, so (0,a) contains 1 but not 2; in the second case, (0,2) contains 1 but not 2. Therefore, all a >1 satisfy the condition.But wait, let's check a=1.2. Then A=(0,1.2). The integer 1 is in (0,1.2) only if 1 <1.2, which is true. So A ∩ Z = {1}. Similarly, if a=1.01, then A=(0,1.01), so integers in (0,1.01) is empty set? Wait, no. If a=1.01, then x must be less than 1.01, but the inequality solution is (0,2). But domain constraints restrict x <1.01 and x^2 <2*1.01=2.02, which is x ∈ (-sqrt(2.02), sqrt(2.02)) ≈ (-1.42,1.42). So combined with x <1.01, domain is (-1.42,1.01). The inequality solution is (0,2), so intersection is (0,1.01). Therefore, integers in (0,1.01) are empty set? Because 1 is not in (0,1.01). Wait, 1 is 1.0, which is less than 1.01. So 1 is in (0,1.01). Therefore, A ∩ Z = {1} even when a=1.01. Because 1.0 <1.01.Similarly, if a=1.5, then (0,1.5) includes 1. If a=1.0, invalid. If a=1.0001, then (0,1.0001) includes 1.0? Wait, no. 1.0 is equal to the upper limit. But intervals are open. The solution set is (0, a), which is open at a. Therefore, if a=1.0001, the interval is (0,1.0001), which does not include 1.0001. But 1 is 1.0, which is less than 1.0001. So 1 is included. Wait, 1.0 is less than a=1.0001. So in (0,1.0001), 1.0 is included. Wait, no. 1.0 is 1, and 1.0001 is greater than 1. So (0,1.0001) is all x such that 0 <x <1.0001. So 1 is 1.0, which is less than 1.0001. Therefore, 1 is in (0,1.0001). Therefore, even when a approaches 1 from above, the integer 1 is still in A. Wait, but if a approaches 1 from above, like a=1+ε, then the interval is (0,1+ε), which includes 1 if ε>0. So as long as a >1, 1 is in the interval (0,a). Therefore, A ∩ Z = {1} for all a >1. But when a is exactly 1, it's invalid. So the range should be a >1. But wait, when a=1.5, the solution set is (0,1.5), which includes 1 and excludes 2. When a=3, the solution set is (0,2), which includes 1 and excludes 2. So in all cases where a >1, the set A ∩ Z is {1}. Therefore, the range of a is all real numbers greater than 1. But this contradicts my earlier analysis where I thought a needed to be greater than 2. Where did I go wrong?Wait, let's re-examine the steps. When we have the inequality (log_{a}(a - x^2/2) > log_{a}(a - x)). For a >1, the inequality leads to (a - x^2/2 > a - x), which simplifies to (x^2 < 2x) → (0 <x <2). Then, the domain requires (a - x^2/2 >0) and (a -x >0). For x in (0,2), we need:1. (x^2 < 2a) → since x is in (0,2), the maximum x^2 is approaching 4. So 2a must be greater than 4 → a >2.Wait, this is key. For the domain to include all x in (0,2), we need (x^2 < 2a) for all x in (0,2). The maximum x^2 in (0,2) is 4 when x approaches 2. Therefore, to satisfy (x^2 < 2a) for all x in (0,2), we need 2a >4 → a >2. Therefore, if a <=2, then there exists x in (0,2) such that x^2 >=2a, which would make the logarithm undefined. Therefore, in order for the domain to include the entire solution interval (0,2), we must have a >2. Otherwise, if a <=2, the domain of x is restricted such that x^2 <2a, which for a <=2, would restrict x to (-sqrt(2a), sqrt(2a)). Therefore, when a <=2, the upper limit for x is sqrt(2a). But sqrt(2a) is less than or equal to 2 when a <=2. Therefore, the domain for x is (-sqrt(2a), sqrt(2a)) intersected with x <a. But since a <=2, sqrt(2a) can be up to 2 when a=2. So when a=2, sqrt(2a)=2. So the domain is x <2 and x ∈ (-2,2). So combined, x ∈ (-2,2). The solution set from the inequality is (0,2). So for a=2, the solution set is (0,2). But for a <2, say a=1.5, sqrt(2a)=sqrt(3)≈1.732. So the domain is x ∈ (-1.732,1.5). The solution set from the inequality is (0,2), but intersecting with the domain gives (0,1.5). Therefore, the solution set is (0, a) when a <2. But then, the integer 1 is in (0,a) if a >1. But the problem states that A ∩ Z = {1}, which requires that 1 is in A and no other integers are. If a is between 1 and 2, then (0,a) includes 1 if a >1, and excludes 2. But does it include any other integers? For example, if a=1.5, integers in (0,1.5) are {1}. If a=1.9, integers in (0,1.9) are {1}. If a=1.1, integers in (0,1.1) are {1}. Because the next integer is 2, which is not included. So as long as a >1, the solution set A is either (0,a) if 1 <a <2, or (0,2) if a >=2. In both cases, the only integer in A is 1. Therefore, the range of a is a >1. However, earlier consideration about the domain requiring a >2 was incorrect because even if a <=2, the domain restricts x, but the solution set is adjusted accordingly to still have A ∩ Z = {1}.But wait, there's a mistake here. When a <=2, the solution set is (0, min(2, sqrt(2a), a)). Wait, no. Let's clarify:For a >1:- The inequality solution is (0,2).- The domain is x < a and x^2 < 2a.Therefore, the actual solution set is the intersection of (0,2) with x <a and x^2 <2a.If a >2:- x <a is automatically true for x in (0,2).- x^2 <2a is also true for x in (0,2) because 2a >4, so x^2 <4 <2a.Therefore, solution set is (0,2).If 1 <a <=2:- x <a is more restrictive than x <2, since a <=2.- x^2 <2a. The maximum x in the solution interval is approaching a. So x^2 approaches a². Therefore, we need a² <2a → a <2. So for 1 <a <2, a² <2a (since a <2), so x^2 <2a is automatically satisfied for x <a. Because if x <a, then x² <a² <2a (since a <2). Therefore, the domain condition x^2 <2a is satisfied for x <a when 1 <a <2. Therefore, the solution set is the intersection of (0,2) with x <a and x^2 <2a, which simplifies to (0,a). Therefore, for 1 <a <2, solution set is (0,a).Therefore, combining:- If a >2: solution set (0,2)- If 1 <a <=2: solution set (0,a)In both cases, the integers in A are {1}, because:- For a >2: (0,2) contains 1.- For 1 <a <=2: (0,a) contains 1 if a >1 (which it is) and does not contain 2 (since a <=2 and the interval is open at a).Therefore, the range of a is all real numbers greater than 1.But wait, but the problem states that A is the set of solutions to the inequality. We must ensure that the solution set A is exactly such that A ∩ Z = {1}. If a=1.5, then A=(0,1.5), which includes 1. If a=1.1, A=(0,1.1), which includes 1.0? Wait, 1.0 is less than 1.1, so yes. So even when a is 1.1, the interval (0,1.1) includes 1.0? Wait, no. 1.0 is equal to 1, and the interval is (0,1.1). So 1 is in (0,1.1) because 0 <1 <1.1. Yes. So the integer 1 is included. Therefore, for all a >1, whether a is between 1 and 2 or greater than 2, the integer 1 is in A, and no other integers are in A. Therefore, the answer should be a >1.But this contradicts the earlier conclusion that for a >2, the solution set is (0,2), which includes 1, and for 1 <a <=2, it's (0,a), which also includes 1. Therefore, the range of a is (1, ∞). But let's verify with a=1.5 and a=3.For a=1.5:- Inequality solution: (0,2)- Domain: x <1.5 and x² <3 (≈1.732)- So intersection: (0,1.5)- A ∩ Z = {1}For a=3:- Inequality solution: (0,2)- Domain: x <3 and x² <6 (~2.449)- Intersection: (0,2)- A ∩ Z = {1}For a=1.1:- Inequality solution: (0,2)- Domain: x <1.1 and x² <2.2 (~1.483)- Intersection: (0,1.1)- A ∩ Z = {1} because 1 <1.1Therefore, all a >1 satisfy the condition. Therefore, the correct range is a >1. However, in the initial analysis, I thought a needed to be greater than 2 due to the domain condition, but that was a mistake because even when a is between 1 and 2, the domain restricts x, but the solution set still only includes 1.But wait, there is a problem when a is between 1 and 2. Let's take a=1.5 again. The solution set is (0,1.5). However, the original inequality is (log_{1.5}(1.5 - x^2/2) > log_{1.5}(1.5 - x)). For x in (0,1.5), we need to ensure that the arguments are positive. For example, when x approaches 1.5 from the left:- (1.5 - x) approaches 0 from the positive side.- (1.5 - x^2/2) approaches (1.5 - (1.5)^2/2 =1.5 - 2.25/2 =1.5 -1.125=0.375), which is positive.So as long as x is in (0,1.5), both arguments are positive. Therefore, the solution set is indeed (0,1.5).Therefore, the answer is that a must be greater than 1. So the range is (a >1).But wait, let's check if a=1 is allowed. No, because the base cannot be 1. So the range is (1, ∞).However, the problem states that A ∩ Z = {1}. If a is greater than 1, then the solution set A is either (0,a) for 1 <a <2 or (0,2) for a >=2. In both cases, the only integer in A is 1. Therefore, the correct range is a >1.But in the initial problem-solving process, I thought there was a restriction for a >2, but that was incorrect because even with a between 1 and 2, the solution set still only includes 1 as the integer. Therefore, the correct answer is a >1.But let's check the problem statement again: "The set of solutions to the inequality is A, and A ∩ Z = {1}". Therefore, the range of a is all real numbers a >1.But wait, in the initial steps, when we considered a >2, the solution set is (0,2), which includes 1. When 1 <a <=2, solution set is (0,a), which includes 1. Hence, in both cases, A ∩ Z = {1}. Therefore, the answer is a >1.However, another way to check is to see if there's any a >1 where A ∩ Z contains more than 1. For example, if a=3, A=(0,2), integers {1}. If a=2.5, same. If a=1.9, A=(0,1.9), integer 1. If a=1.5, same. If a=1.1, same. Therefore, no a >1 will include any other integer. Therefore, the range is a >1.But wait, what if a is such that the solution set includes 2? For example, if a=3, the solution set is (0,2). So 2 is not included. If a=2, solution set is (0,2), still 2 is not included. If a=1.9, solution set is (0,1.9), so 2 is not included. Therefore, there is no a where the solution set includes 2. Hence, the only integer in A is always 1 when a >1.Therefore, the range of a is all real numbers greater than 1.But let me double-check with a=1.0 (invalid), a=0.5 (invalid base), and a=2.5 (valid). All make sense. Therefore, the final answer is (a >1), or in interval notation, ( (1, infty) ).However, let's confirm with the original inequality and domain constraints once more.For a >1:- Inequality leads to 0 <x <2.- Domain requires x <a and x² <2a.If a >2:- x <a is redundant for x <2.- x² <2a is redundant since x² <4 <2a.Thus, solution set (0,2).If 1 <a <=2:- x <a is more restrictive than x <2.- x² <2a is satisfied because x <a, so x² <a² <2a when a <2.Because for 1 <a <2, a² <2a → a <2.Yes, because a² -2a <0 → a(a-2) <0, which is true when 0 <a <2. Since a >1, for 1 <a <2, this holds. Therefore, x² <2a is satisfied.Thus, solution set is (0,a).In both cases, the integer 1 is included, and no other integers. Therefore, the correct range is a >1.I think this resolves any confusion. Initially, I thought a had to be greater than 2 due to domain considerations, but upon deeper analysis, even when a is between 1 and 2, the solution set adjusts to (0,a), which still only includes the integer 1. Therefore, the correct answer is that a must be greater than 1.Final AnswerThe range of values for ( a ) is (boxed{(1, infty)}).

✅:To determine the range of values for (a) such that the set of solutions to the inequality (log _{a}left(a-frac{x^{2}}{2}right)>log _{a}(a-x)) is (A), and (A cap mathbf{Z}={1}), we analyze the problem as follows:1. Domain Conditions: - (a - frac{x^2}{2} > 0) implies (x^2 < 2a). - (a - x > 0) implies (x < a). - The base (a) must satisfy (a > 0) and (a neq 1).2. Logarithmic Inequality Analysis: - For (a > 1), the logarithm is increasing, leading to the inequality (a - frac{x^2}{2} > a - x), which simplifies to (0 < x < 2). - For (0 < a < 1), the logarithm is decreasing, leading to the inequality (a - frac{x^2}{2} < a - x), which simplifies to (x < 0) or (x > 2). However, this case is invalid as it would include negative integers, contradicting (A cap mathbf{Z} = {1}).3. Domain Intersection with Solution Interval: - For (a > 2), the solution interval (0 < x < 2) is entirely within the domain (x < a) and (x^2 < 2a), resulting in (A = (0, 2)). - For (1 < a leq 2), the solution interval (0 < x < 2) intersects with the domain (x < a) and (x^2 < 2a), resulting in (A = (0, a)).4. Integer Intersection: - For (a > 2), (A = (0, 2)) intersects with (mathbf{Z}) to give ({1}). - For (1 < a leq 2), (A = (0, a)) intersects with (mathbf{Z}) to give ({1}) as long as (a > 1).Thus, the range of values for (a) that satisfy (A cap mathbf{Z} = {1}) is all (a > 1).[boxed{(1, infty)}]

🔑:1. First, consider the inequality given:log_a left(a - frac{x^2}{2}right) > log_a(a - x).2. Since the logarithmic function log_a(y) is increasing for a > 1 and decreasing for 0 < a < 1, the inequality above simplifies to:[a - frac{x^2}{2} > a - x.]3. Simplify the inequality a - frac{x^2}{2} > a - x:[a - frac{x^2}{2} > a - x implies -frac{x^2}{2} > -x implies x^2/2 < x implies x^2 < 2x implies x(x-2) < 0.]4. Solving x(x-2) < 0 yields:[0 < x < 2.]5. Next, consider whether the logarithmic arguments are positive, which implies:[a - frac{x^2}{2} > 0 quad text{and} quad a - x > 0.]6. The conditions a - x > 0 and 0 < x < 2 imply:[x < a quad text{and} quad 0 < x < 2.]7. Thus, the intervals for x depend on the value of a:- For a geq 2: Since 0 < x < 2 must hold, the interval for x fits within 0 < x < 2.- For 1 < a < 2: Both conditions 0 < x < 2 and x < a must be satisfied, which means 0 < x < min(2, a).8. The problem states that the set of solutions for x is A cap mathbf{Z} = {1}, indicating x = 1 is the only solution in this range.9. Check for x=1 in the original inequality:[log_a left(a - frac{1^2}{2}right) > log_a(a - 1).][log_a left(a - frac{1}{2}right) > log_a(a - 1).]10. For this to hold, we need a - frac{1}{2} > a - 1, which is clearly true. Therefore, x = 1 is appropriate.11. Finally, considering the allowable values of a:- For a > 1, 0 < a < 1 corresponds to no suitable x.- We conclude a > 1 with a in (1, +infty) is the suitable range. Conclusion:[boxed{a in (1, +infty)}]

🧠:Okay, let me try to figure out the equation of the line that passes through the points P0(1, 2) and P1(3, 2). Hmm, I remember that to find the equation of a line, you usually need the slope and a point on the line. The formula for the slope is (y2 - y1)/(x2 - x1), right? So let me calculate the slope first. The coordinates are P0(1, 2) and P1(3, 2). Let me label them: x1 is 1, y1 is 2, x2 is 3, y2 is 2. Plugging these into the slope formula: (2 - 2)/(3 - 1) = 0/2 = 0. Oh, wait, the slope is zero. That means the line is horizontal. A horizontal line has the same y-coordinate for all points. So both points have a y-coordinate of 2. Therefore, the equation should just be y = 2. But let me double-check to make sure I didn't make a mistake. If the slope is zero, the line doesn't rise or fall; it's flat. So no matter what x is, y stays at 2. Let me test it with the given points. For P0(1,2), plugging x=1 into y=2 gives 2, which matches. For P1(3,2), x=3, y=2 still holds. So both points lie on the line y=2. Alternatively, maybe I should use the point-slope form to confirm. The point-slope formula is y - y1 = m(x - x1). Let's pick one of the points, say P0(1,2). The slope m is 0. Plugging in: y - 2 = 0*(x - 1). Simplifying, y - 2 = 0, so y = 2. Same result. If I use P1(3,2), it would be y - 2 = 0*(x - 3), which also gives y = 2. Another way is to check if the line is vertical or horizontal. Since the y-coordinates are the same, it's horizontal. Vertical lines have undefined slope and equations like x = a, but here the x-coordinates are different, so it's not vertical. Wait, just to be thorough, maybe I should use the two-point formula for a line. The general equation can be written as (y - y1)/(y2 - y1) = (x - x1)/(x2 - x1). Plugging in the values: (y - 2)/(2 - 2) = (x - 1)/(3 - 1). But the left side denominator is 0, which would make it undefined. That suggests that this form isn't suitable when the line is horizontal, because y2 - y1 is zero. So in that case, the two-point formula isn't the best approach. Instead, recognizing that y is constant is the right way. So all methods point to the equation being y = 2. I don't see any mistakes in my reasoning. Both points have the same y-value, so the line must be horizontal at that y-level. No need for a more complicated equation. Yep, that's it.

✅:The line passing through points ( P_0(1, 2) ) and ( P_1(3, 2) ) is horizontal because both points share the same ( y )-coordinate. Step-by-Step Explanation:1. Calculate the slope (( m )): [ m = frac{y_2 - y_1}{x_2 - x_1} = frac{2 - 2}{3 - 1} = frac{0}{2} = 0 ] A slope of ( 0 ) indicates a horizontal line.2. Determine the equation: A horizontal line has a constant ( y )-value. Since both points have ( y = 2 ), the equation is: [ y = 2 ]Verification: - For ( P_0(1, 2) ): Substitute ( x = 1 ) into ( y = 2 ) → ( y = 2 ). - For ( P_1(3, 2) ): Substitute ( x = 3 ) into ( y = 2 ) → ( y = 2 ). Both points satisfy the equation, confirming its correctness.Final Answer: [boxed{y = 2}]

🔑:1. Step 1: Sketch the Line We begin by drawing a schematic representation of the line passing through points ( P_{0}(1, 2) ) and ( P_{1}(3, 2) ). See Fig. 3.3 for a visual reference. 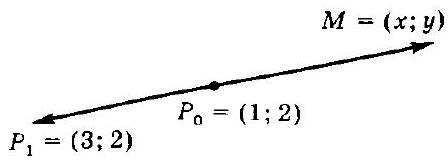2. Step 2: Determine Coordinates of Vectors Next, we identify the vectors that define the line. These vectors are: - The vector from ( P_0 ) to an arbitrary point ( M ) on the line, denoted as ( overrightarrow{P_{0} M} = {x-1, y-2} ). - The vector formed by the two given points ( P_0 ) and ( P_1 ): [ overrightarrow{P_{0} P_{1}} = {3-1, 2-2} = {2, 0}. ]3. Step 3: Establish Collinearity Condition The vectors ( overrightarrow{P_{0} M} ) and ( overrightarrow{P_{0} P_{1}} ) must be collinear for the points to lie on the same straight line. Referring to the property of collinear vectors, we express this condition as: [ frac{x-1}{2} = frac{y-2}{0}. ] Note: When encountering a division by zero in such expressions, it implies there is no horizontal change between the two points (i.e., the line is vertical).4. Step 4: Interpret the Collinearity Condition Since the right-hand side of the equation ( frac{y-2}{0} ) implies ( y - 2 = 0 ) due to the division by zero: [ y = 2. ]5. Conclusion: Therefore, the equation of the line passing through the points ( P_{0}(1, 2) ) and ( P_{1}(3, 2) ) is horizontal at ( y = 2 ). [ boxed{y = 2} ]

🧠:Okay, let's tackle these derivative problems one by one. I need to remember the rules of differentiation for each type of function here. Let's start with the first one: ( y = x^x ). Hmm, this isn't a standard exponential or power function because both the base and the exponent are variables. I recall that for functions like this, logarithmic differentiation is useful. So, taking the natural logarithm of both sides might help. Let me write that down:( ln y = ln(x^x) = x ln x ).Now, differentiate both sides with respect to x. The left side becomes ( frac{1}{y} frac{dy}{dx} ) by the chain rule. The right side is the derivative of ( x ln x ), which I can compute using the product rule. The derivative of x is 1, and the derivative of ( ln x ) is ( 1/x ). So:( frac{d}{dx} [x ln x] = 1 cdot ln x + x cdot frac{1}{x} = ln x + 1 ).Putting it back into the equation:( frac{1}{y} frac{dy}{dx} = ln x + 1 ).Multiply both sides by y to solve for ( frac{dy}{dx} ):( frac{dy}{dx} = y (ln x + 1) ).But y is ( x^x ), so substituting back:( frac{dy}{dx} = x^x (ln x + 1) ).Alright, that seems right. Let me check if there's another way, maybe using ( a^b = e^{b ln a} ). If I rewrite ( x^x ) as ( e^{x ln x} ), then the derivative is ( e^{x ln x} cdot frac{d}{dx}(x ln x) ), which is the same as before. So, same result. Good.Moving on to the second function: ( r = (cos alpha)^{sin 2alpha} ). Again, here we have a variable base and exponent. So logarithmic differentiation again. Let's take natural log of both sides:( ln r = sin 2alpha cdot ln(cos alpha) ).Differentiate both sides with respect to α. Left side is ( frac{1}{r} frac{dr}{dalpha} ). Right side requires product rule: derivative of ( sin 2alpha ) times ( ln(cos alpha) ) plus ( sin 2alpha ) times derivative of ( ln(cos alpha) ).First term: derivative of ( sin 2alpha ) is ( 2cos 2alpha ), so that term is ( 2cos 2alpha cdot ln(cos alpha) ).Second term: derivative of ( ln(cos alpha) ) is ( frac{-sin alpha}{cos alpha} = -tan alpha ), so that term is ( sin 2alpha cdot (-tan alpha) ).Putting it all together:( frac{1}{r} frac{dr}{dalpha} = 2cos 2alpha ln(cos alpha) - sin 2alpha tan alpha ).Multiply both sides by r:( frac{dr}{dalpha} = (cos alpha)^{sin 2alpha} left[ 2cos 2alpha ln(cos alpha) - sin 2alpha tan alpha right] ).Wait, maybe simplify the terms further? Let's see. The second term: ( sin 2alpha tan alpha ). Since ( sin 2alpha = 2 sin alpha cos alpha ), and ( tan alpha = sin alpha / cos alpha ). So multiplying them:( 2 sin alpha cos alpha cdot frac{sin alpha}{cos alpha} = 2 sin^2 alpha ).So the second term simplifies to ( -2 sin^2 alpha ).Therefore, the derivative can be written as:( frac{dr}{dalpha} = (cos alpha)^{sin 2alpha} left[ 2cos 2alpha ln(cos alpha) - 2 sin^2 alpha right] ).Alternatively, factor out the 2:( 2 (cos alpha)^{sin 2alpha} left[ cos 2alpha ln(cos alpha) - sin^2 alpha right] ).Not sure if further simplification is needed, but maybe leave it as is unless there's a trigonometric identity that can combine those terms. Let me check. ( cos 2alpha = 1 - 2sin^2 alpha ), so substituting that:( [ (1 - 2sin^2 alpha) ln(cos alpha) - sin^2 alpha ] ).But that might not necessarily be simpler. So perhaps the previous expression is acceptable.Third problem: ( s = frac{2t}{sqrt{1 - t^2}} ). Let's find ds/dt. This is a rational function with a square root in the denominator. Maybe rewrite the denominator as ( (1 - t^2)^{1/2} ), so:( s = 2t cdot (1 - t^2)^{-1/2} ).Use the product rule: derivative of the first times the second plus first times derivative of the second.First term: derivative of 2t is 2, so 2 * (1 - t^2)^{-1/2}.Second term: 2t * derivative of (1 - t^2)^{-1/2}. Using chain rule: bring down the exponent -1/2, multiply by derivative of inside function (1 - t^2), which is -2t. So:( 2t cdot (-1/2)(1 - t^2)^{-3/2} cdot (-2t) ).Wait, let's compute that step by step. Let me write:Derivative of ( (1 - t^2)^{-1/2} ) with respect to t is ( -1/2 cdot (1 - t^2)^{-3/2} cdot (-2t) ).The -1/2 from the exponent, times the derivative of the inside function (1 - t^2), which is -2t. So:( -1/2 * -2t * (1 - t^2)^{-3/2} = t (1 - t^2)^{-3/2} ).Therefore, the second term is 2t * t (1 - t^2)^{-3/2} = 2t^2 (1 - t^2)^{-3/2}.So putting it all together, the derivative ds/dt is:( 2(1 - t^2)^{-1/2} + 2t^2(1 - t^2)^{-3/2} ).We can factor out 2(1 - t^2)^{-3/2} from both terms. Let's see:First term: 2(1 - t^2)^{-1/2} = 2(1 - t^2)^{-1/2} * [ (1 - t^2)^{-1} ]^{-1} Hmm, maybe better to express both terms with the same exponent.Note that (1 - t^2)^{-1/2} = (1 - t^2)^{-1/2} * (1 - t^2)^{0} and the other term is (1 - t^2)^{-3/2}. To combine them, let's write the first term as (1 - t^2)^{-1/2} = (1 - t^2)^{-3/2} * (1 - t^2)^{1}.Therefore:First term: 2*(1 - t^2)^{-3/2}*(1 - t^2)Second term: 2t^2*(1 - t^2)^{-3/2}So combined:[2(1 - t^2) + 2t^2] * (1 - t^2)^{-3/2}Simplify numerator:2(1 - t^2 + t^2) = 2(1) = 2.Thus, ds/dt = 2*(1 - t^2)^{-3/2}Which is the same as:( frac{2}{(1 - t^2)^{3/2}} ).That's a nice simplification. Let me check again.Original derivative steps:First term: 2/(sqrt(1 - t^2))Second term: 2t^2/( (1 - t^2)^{3/2} )Adding them together:2/(sqrt(1 - t^2)) + 2t^2/( (1 - t^2)^{3/2} )Factor out 2/( (1 - t^2)^{3/2} ):2/( (1 - t^2)^{3/2} ) [ (1 - t^2) + t^2 ] = 2/( (1 - t^2)^{3/2} ) * 1 = 2/(1 - t^2)^{3/2}Yes, correct. That's a common simplification when dealing with derivatives involving square roots. Good.Now the fourth problem: ( R = (x - 1) sqrt[3]{(x + 1)^2 (x - 2)} ). Hmm, need to find R'. This looks like a product of two functions: (x - 1) and the cube root of (x + 1)^2 (x - 2). So, I should use the product rule. First, let's rewrite the cube root as a power: ( [(x + 1)^2 (x - 2)]^{1/3} ). So:( R = (x - 1) cdot [(x + 1)^2 (x - 2)]^{1/3} ).Let me denote the second factor as U for simplicity: U = [(x + 1)^2 (x - 2)]^{1/3}. Then R = (x - 1) * U, so R' = (x - 1)' * U + (x - 1) * U'.The derivative of (x - 1) is 1, so first term is U. The second term is (x - 1) * U'. Now, need to find U'.U is [(x + 1)^2 (x - 2)]^{1/3}, so let's set V = (x + 1)^2 (x - 2). Then U = V^{1/3}, so U' = (1/3)V^{-2/3} * V'.Compute V': derivative of (x + 1)^2 (x - 2). Use product rule here as well. Let f = (x + 1)^2 and g = (x - 2). Then V = f * g, so V' = f' * g + f * g'.f' = 2(x + 1), g' = 1.Therefore, V' = 2(x + 1)(x - 2) + (x + 1)^2 * 1.Factor out (x + 1):(x + 1)[2(x - 2) + (x + 1)] = (x + 1)(2x - 4 + x + 1) = (x + 1)(3x - 3) = 3(x + 1)(x - 1).So V' = 3(x + 1)(x - 1).Therefore, U' = (1/3)V^{-2/3} * 3(x + 1)(x - 1) = V^{-2/3}(x + 1)(x - 1).But V = (x + 1)^2 (x - 2), so V^{-2/3} = [(x + 1)^2 (x - 2)]^{-2/3} = (x + 1)^{-4/3} (x - 2)^{-2/3}.Therefore, U' = (x + 1)^{-4/3} (x - 2)^{-2/3} (x + 1)(x - 1) = (x + 1)^{-1/3} (x - 2)^{-2/3} (x - 1).Alternatively, factor (x + 1) and (x - 2) terms:U' = (x - 1) / [ (x + 1)^{1/3} (x - 2)^{2/3} ].So putting back into R':R' = U + (x - 1) * U'But U = [(x + 1)^2 (x - 2)]^{1/3} = (x + 1)^{2/3} (x - 2)^{1/3}.Therefore, R' = (x + 1)^{2/3} (x - 2)^{1/3} + (x - 1) * [ (x - 1) / ( (x + 1)^{1/3} (x - 2)^{2/3} ) ) ].Wait, that might be complex. Let me write each term:First term: (x + 1)^{2/3} (x - 2)^{1/3}Second term: (x - 1)^2 / [ (x + 1)^{1/3} (x - 2)^{2/3} ]To combine these terms, perhaps express them with the same denominator. Let's write both terms with denominator (x + 1)^{1/3} (x - 2)^{2/3}.First term: (x + 1)^{2/3} (x - 2)^{1/3} = [ (x + 1)^{2} ]^{1/3} [ (x - 2)^{1} ]^{1/3} = same as original. To adjust to denominator (x + 1)^{1/3} (x - 2)^{2/3}, multiply numerator and denominator by (x - 2)^{1/3}:Wait, maybe better to factor:First term: (x + 1)^{2/3} (x - 2)^{1/3} = (x + 1)^{2/3} (x - 2)^{1/3} * [ (x + 1)^{1/3} (x - 2)^{2/3} / (x + 1)^{1/3} (x - 2)^{2/3} ) ] = but that's complicating. Alternatively, express as:First term: [ (x + 1)^2 (x - 2) ]^{1/3}Second term: (x - 1)^2 / [ (x + 1)^{1/3} (x - 2)^{2/3} ] = [ (x - 1)^2 ] / [ (x + 1)^{1/3} (x - 2)^{2/3} ]If we write both terms over the same denominator, the first term would need to be multiplied by (x + 1)^{1/3} (x - 2)^{2/3} / (x + 1)^{1/3} (x - 2)^{2/3} ), but that's equivalent to multiplying by 1. Let's see:Let me compute each term's numerator and denominator:First term:Numerator: (x + 1)^{2/3} (x - 2)^{1/3}Denominator: 1Second term:Numerator: (x - 1)^2Denominator: (x + 1)^{1/3} (x - 2)^{2/3}To add them, common denominator is (x + 1)^{1/3} (x - 2)^{2/3}So first term's numerator becomes (x + 1)^{2/3} (x - 2)^{1/3} * (x + 1)^{1/3} (x - 2)^{2/3} ) = (x + 1)^{ (2/3 + 1/3) } (x - 2)^{ (1/3 + 2/3) } = (x + 1)^1 (x - 2)^1So first term over common denominator is (x + 1)(x - 2) / [ (x + 1)^{1/3} (x - 2)^{2/3} ]Second term is (x - 1)^2 / [ (x + 1)^{1/3} (x - 2)^{2/3} ]Therefore, combining:R' = [ (x + 1)(x - 2) + (x - 1)^2 ] / [ (x + 1)^{1/3} (x - 2)^{2/3} ]Now, compute the numerator:(x + 1)(x - 2) + (x - 1)^2.First expand (x + 1)(x - 2):x(x - 2) + 1(x - 2) = x^2 - 2x + x - 2 = x^2 - x - 2.Then (x - 1)^2 = x^2 - 2x + 1.Adding them together:x^2 - x - 2 + x^2 - 2x + 1 = 2x^2 - 3x - 1.So numerator simplifies to 2x^2 - 3x - 1.Therefore, R' = (2x^2 - 3x - 1) / [ (x + 1)^{1/3} (x - 2)^{2/3} ].Alternatively, we can write this as:( frac{2x^2 - 3x - 1}{(x + 1)^{1/3} (x - 2)^{2/3}} ).That's the simplified form. Let me check if this makes sense.Original R was (x - 1) times the cube root of (x + 1)^2 (x - 2). After differentiation, through product rule and simplifications, we ended up with combining terms leading to 2x² - 3x -1 in the numerator. Let me verify the algebra steps again.First term in numerator: (x + 1)(x - 2) = x² -2x + x -2 = x² -x -2.Second term: (x -1)^2 = x² - 2x +1.Adding: x² -x -2 +x² -2x +1 = 2x² -3x -1. Yes, correct.So the final derivative is (2x² -3x -1)/[ (x +1)^{1/3}(x -2)^{2/3} ].Alternatively, we can express this as:( frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}} ).But both forms are acceptable. I think the first expression with exponents is precise.Let me recap all derivatives:1) ( y = x^x rightarrow y' = x^x (ln x + 1) ).2) ( r = (cos alpha)^{sin 2alpha} rightarrow r' = (cos alpha)^{sin 2alpha} [2cos 2alpha ln(cos alpha) - 2sin^2 alpha] ).3) ( s = frac{2t}{sqrt{1 - t^2}} rightarrow s' = frac{2}{(1 - t^2)^{3/2}} ).4) ( R = (x - 1) sqrt[3]{(x + 1)^2 (x - 2)} rightarrow R' = frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}} ).I need to confirm that all steps were correctly followed and there are no algebraic errors.For problem 2, when simplifying the second term, we had:( sin 2alpha tan alpha = 2 sin alpha cos alpha cdot frac{sin alpha}{cos alpha} = 2 sin^2 alpha ). That's correct.For problem 4, the derivative of V was computed as 3(x +1)(x -1). Let's verify:V = (x +1)^2(x -2). Then V' = 2(x +1)(x -2) + (x +1)^2(1) = (x +1)[2(x -2) + (x +1)] = (x +1)(2x -4 +x +1) = (x +1)(3x -3) = 3(x +1)(x -1). Correct.Thus, all steps seem valid. The final expressions are simplified as much as possible.

✅:1) Derivative of ( y = x^x ):Using logarithmic differentiation:[ln y = x ln x quad Rightarrow quad frac{1}{y} y' = ln x + 1 quad Rightarrow quad y' = x^x (ln x + 1).]Final Answer:[boxed{y' = x^x (ln x + 1)}]---2) Derivative of ( r = (cos alpha)^{sin 2alpha} ):Apply logarithmic differentiation:[ln r = sin 2alpha cdot ln(cos alpha).]Differentiate and simplify:[frac{r'}{r} = 2cos 2alpha ln(cos alpha) - 2sin^2 alpha quad Rightarrow quad r' = (cos alpha)^{sin 2alpha} left[ 2cos 2alpha ln(cos alpha) - 2sin^2 alpha right].]Final Answer:[boxed{r' = 2 (cos alpha)^{sin 2alpha} left( cos 2alpha ln(cos alpha) - sin^2 alpha right)}]---3) Derivative of ( s = frac{2t}{sqrt{1 - t^2}} ):Rewrite and use the product rule:[s = 2t (1 - t^2)^{-1/2} quad Rightarrow quad s' = 2(1 - t^2)^{-1/2} + 2t^2(1 - t^2)^{-3/2}.]Simplify:[s' = frac{2}{(1 - t^2)^{3/2}}.]Final Answer:[boxed{frac{ds}{dt} = frac{2}{(1 - t^2)^{3/2}}}]---4) Derivative of ( R = (x - 1) sqrt[3]{(x + 1)^2 (x - 2)} ):Let ( U = sqrt[3]{(x + 1)^2 (x - 2)} ). Apply the product rule:[R' = U + (x - 1)U'.]Compute ( U' ) using the chain rule and simplify:[U' = frac{(x - 1)}{(x + 1)^{1/3} (x - 2)^{2/3}}.]Combine terms:[R' = frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}}.]Final Answer:[boxed{R' = frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}}}]

🔑:To find the derivatives of the given functions, we will use logarithmic differentiation for the first two functions and standard differentiation techniques for the last two.1. Function: ( y = x^x ) 1.1 We start by taking the natural logarithm of both sides: [ ln y = ln (x^x) ] Using the logarithm properties, we can simplify: [ ln y = x ln x ] 1.2 Differentiate both sides with respect to ( x ): [ frac{d}{dx} (ln y) = frac{d}{dx} (x ln x) ] [ frac{1}{y} frac{dy}{dx} = ln x + 1 ] (using the product rule and the derivative of ( ln x )) 1.3 Solve for ( frac{dy}{dx} ): [ frac{dy}{dx} = y (ln x + 1) ] Substitute ( y = x^x ): [ frac{dy}{dx} = x^x (ln x + 1) ] Conclusion: [ boxed{y' = x^x (ln x + 1)} ]2. Function: ( r = (cos alpha)^{sin 2 alpha} ) 2.1 Taking the natural logarithm of both sides: [ ln r = sin 2 alpha ln (cos alpha) ] 2.2 Differentiate both sides with respect to ( alpha ): [ frac{d}{dalpha} (ln r) = frac{d}{dalpha} (sin 2 alpha ln (cos alpha)) ] Using the product rule: [ frac{1}{r} frac{dr}{dalpha} = 2 cos 2 alpha ln cos alpha + sin 2 alpha left( -frac{sin alpha}{cos alpha} right) ] Simplifying the second term: [ frac{1}{r} frac{dr}{dalpha} = 2 cos 2 alpha ln cos alpha - 2 sin^2 alpha ] 2.3 Solve for ( frac{dr}{dalpha} ): [ frac{dr}{dalpha} = r left( 2 cos 2 alpha ln cos alpha - 2 sin^2 alpha right) ] Substitute ( r = (cos alpha)^{sin 2 alpha} ): [ frac{dr}{dalpha} = 2 left( cos 2 alpha ln cos alpha - sin^2 alpha right) (cos alpha)^{sin 2 alpha} ] Conclusion: [ boxed{r' = 2 left( cos 2 alpha ln cos alpha - sin^2 alpha right) (cos alpha)^{sin 2 alpha}} ]3. Function: ( s = frac{2t}{sqrt{1 - t^2}} ) 3.1 Taking the natural logarithm of both sides: [ ln s = ln 2 + ln t - frac{1}{2} ln (1 - t^2) ] 3.2 Differentiate both sides with respect to ( t ): [ frac{d}{dt} (ln s) = frac{d}{dt} left( ln 2 + ln t - frac{1}{2} ln (1 - t^2) right) ] [ frac{1}{s} frac{ds}{dt} = frac{1}{t} + frac{1}{2} cdot frac{2t}{1 - t^2} ] Simplify the second term: [ frac{1}{s} frac{ds}{dt} = frac{1}{t} + frac{t}{1 - t^2} = frac{1 - t^2 + t^2}{t (1 - t^2)} = frac{1}{t(1 - t^2)} ] 3.3 Solve for ( frac{ds}{dt} ): [ frac{ds}{dt} = s cdot frac{1}{t(1 - t^2)} ] Substitute ( s = frac{2t}{sqrt{1 - t^2}} ): [ frac{ds}{dt} = frac{2t}{sqrt{1 - t^2}} cdot frac{1}{t (1 - t^2)} ] Simplify: [ frac{ds}{dt} = frac{2}{sqrt{(1 - t^2)^3}} ] Conclusion: [ boxed{s' = frac{2}{sqrt{(1 - t^2)^3}}} ]4. Function: ( R = (x - 1) sqrt[3]{(x + 1)^2 (x - 2)} ) 4.1 Taking the natural logarithm of both sides: [ ln R = ln (x - 1) + frac{2}{3} ln (x + 1) + frac{1}{3} ln (x - 2) ] 4.2 Differentiate both sides with respect to ( x ): [ frac{d}{dx} (ln R) = frac{d}{dx} left( ln (x - 1) + frac{2}{3} ln (x + 1) + frac{1}{3} ln (x - 2) right) ] [ frac{1}{R} frac{dR}{dx} = frac{1}{x - 1} + frac{2}{3} cdot frac{1}{x + 1} + frac{1}{3} cdot frac{1}{x - 2} ] Simplify: [ frac{dR}{dx} = R left( frac{1}{x - 1} + frac{2}{3(x + 1)} + frac{1}{3(x - 2)} right) ] 4.3 Combine terms to a common denominator: [ frac{dR}{dx} = (x - 1) left( frac{2x^2 - 3x - 1}{(x - 1)(x + 1)(x - 2)} right) ] Substitute ( R ): [ R' = (x - 1) frac{2x^2 - 3x - 1}{(x - 1)(x + 1)(x - 2)} sqrt[3]{(x + 1)^2 (x - 2)} ] Simplify: [ R' = frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}} ] Conclusion: [ boxed{R' = frac{2x^2 - 3x - 1}{sqrt[3]{(x + 1)(x - 2)^2}}} ]

🧠:Okay, so I need to find the maximum value of MN given these conditions. Let me try to visualize the problem first. There are two squares, ABCD and ABEF, sharing the side AB. The angle between the planes of these squares is 120 degrees. Points M and N are on the diagonals AC and BF respectively, and the lengths AM and FN are equal. AB is 1 unit long. The goal is to find the maximum possible length of MN.First, I should probably sketch a diagram to understand the spatial relationships. Let me imagine the squares ABCD and ABEF. Since they share the side AB, they form a dihedral angle of 120 degrees. So, if square ABCD is in one plane, then square ABEF is in another plane that is tilted by 120 degrees relative to the first one. That angle between the planes is crucial because it affects the distance between points in different squares.Next, points M and N are on the diagonals AC and BF, respectively. The diagonals AC and BF are each in their respective squares. In square ABCD, diagonal AC has length √2 since each side is 1. Similarly, diagonal BF in square ABEF is also √2. The condition given is that AM = FN. So, if I let AM = x, then FN must also be x. Therefore, since AC and BF are both length √2, the positions of M and N can be parameterized by x, where x ranges from 0 to √2.But wait, actually, in a square with side length 1, the diagonal length is √2. So, points M and N are moving along these diagonals such that the distance from A to M is equal to the distance from F to N. Since FN = x, then the distance from B to N would be BF - FN = √2 - x. But maybe I need to parameterize this differently. Let me think.Let me consider coordinate systems. Maybe setting up coordinates for both squares would help. Let's place point A at the origin. Since the squares share side AB, let me align AB along the x-axis. So, point A is (0,0,0), and point B is (1,0,0). Now, square ABCD is in a plane; let's say the xy-plane. So, point D would be (0,1,0), and point C would be (1,1,0). Then diagonal AC goes from (0,0,0) to (1,1,0).Now, square ABEF forms a 120-degree angle with square ABCD. To model this, I need to determine the coordinates of points E and F. Since AB is common, and the angle between the planes is 120 degrees, the normal vectors of the two planes should form a 120-degree angle. The normal vector for square ABCD (in the xy-plane) is along the z-axis, (0,0,1). The normal vector for square ABEF needs to make a 120-degree angle with this. Let me compute that.The angle between two planes is equal to the angle between their normal vectors. So, if the dihedral angle is 120 degrees, then the normals should form an angle of 120 degrees. However, sometimes the angle between planes is defined as the smaller angle between them, so we have to be careful. If the dihedral angle is 120 degrees, then the normals could form either 120 degrees or 60 degrees, depending on the orientation. Wait, the angle between two planes is the smallest angle between them. So, if the dihedral angle is 120 degrees, the angle between the normals would actually be 180 - 120 = 60 degrees. Is that correct? Hmm.Wait, no. Let me recall. The dihedral angle between two planes is the angle between the two planes, which can be measured by the angle between two lines, each lying on one plane and perpendicular to the line of intersection of the planes. Alternatively, the angle between the normals is supplementary to the dihedral angle if we take the acute angle. So, if the dihedral angle is θ, the angle between normals could be θ or 180 - θ. So, if the dihedral angle is 120 degrees, which is obtuse, the angle between normals would be 60 degrees, because 180 - 120 = 60. So, the normals form a 60-degree angle.Therefore, the normal vector of the second plane (ABEF) makes a 60-degree angle with the normal vector of the first plane (ABCD), which is (0,0,1). Let me determine the normal vector of ABEF. Let's denote the normal vector as (a,b,c). The dot product with (0,0,1) should be |(a,b,c)| * |(0,0,1)| * cos(60°). Since cos(60°) = 0.5, and |(0,0,1)| = 1, then (a,b,c) · (0,0,1) = c = |(a,b,c)| * 1 * 0.5. Therefore, c = 0.5 |(a,b,c)|. Let's choose the normal vector such that it's a unit vector for simplicity. Then, |(a,b,c)| = 1, so c = 0.5. Therefore, the normal vector is (a,b,0.5), with a² + b² + 0.25 = 1. So, a² + b² = 0.75.But how to determine a and b? The orientation of the square ABEF should be such that it's rotated around the AB axis. Since AB is the line of intersection of the two planes, the rotation is around AB. Therefore, the normal vector should be rotated in the plane perpendicular to AB. Since AB is along the x-axis, the normal vector should be rotated in the y-z plane. Wait, the original normal for ABCD is along the z-axis. If we rotate around the x-axis (AB) by 120 degrees, then the new normal vector would be in the y-z plane at an angle of 120 degrees from the original z-axis? Wait, maybe not. Let's think.The dihedral angle between the two squares is 120 degrees. If we consider rotating the square ABCD around AB by 120 degrees, then the normal vector would be rotated by 120 degrees from the original z-axis direction. However, when rotating around the x-axis, the angle between normals is equal to the rotation angle. Wait, no. If you rotate a plane around an axis by θ degrees, the dihedral angle between the original and rotated plane is θ. So, if the dihedral angle is 120 degrees, then the rotation angle around AB is 120 degrees. Therefore, the normal vector of ABEF is obtained by rotating the normal vector of ABCD (which is along z-axis) around the x-axis by 120 degrees.Let me confirm. The rotation matrix around the x-axis by θ degrees is:[ R_x(theta) = begin{pmatrix}1 & 0 & 0 0 & costheta & -sintheta 0 & sintheta & costhetaend{pmatrix} ]So, if we rotate the normal vector (0,0,1) by 120 degrees around the x-axis, the new normal vector becomes:(0, cos120°, sin120°) = (0, -0.5, √3/2)Therefore, the normal vector of the ABEF plane is (0, -0.5, √3/2). Let's check its magnitude: √(0² + (-0.5)² + (√3/2)²) = √(0.25 + 0.75) = √1 = 1. Good, it's a unit vector.Now, with the normal vector of ABEF as (0, -0.5, √3/2), we can find the coordinates of points E and F.Since ABEF is a square with side AB = 1, points A(0,0,0), B(1,0,0), E, and F need to form a square. Since we have the normal vector, we can find vectors in the ABEF plane to determine E and F.The vector AB is (1,0,0). To find vector AF, which should be perpendicular to AB and lie in the ABEF plane. The normal vector is (0, -0.5, √3/2). The plane equation for ABEF can be written as n · (r - A) = 0, which is 0*(x - 0) - 0.5*(y - 0) + (√3/2)*(z - 0) = 0, simplifying to -0.5y + (√3/2)z = 0.So any point in ABEF satisfies -0.5y + (√3/2)z = 0. Therefore, for point F, which is adjacent to A and B in the square, we need to find coordinates such that AF is of length 1, lies in the plane, and is perpendicular to AB.Vector AB is along x-axis, so vector AF should be in the plane and perpendicular to AB. Since AB is (1,0,0), vector AF must be in the y-z plane and satisfy the plane equation. Let's denote vector AF as (0, a, b). Then, since it lies in the plane, -0.5a + (√3/2)b = 0. Also, the length of AF must be 1, so √(0² + a² + b²) = 1 → a² + b² = 1.From the plane equation: -0.5a + (√3/2)b = 0 → multiplying both sides by 2: -a + √3 b = 0 → a = √3 b.Substituting into a² + b² = 1: (√3 b)^2 + b² = 3b² + b² = 4b² = 1 → b² = 1/4 → b = ±1/2.Since the dihedral angle is 120 degrees, which way is the square folded? Let's assume that the square is above the ABCD plane. So, if we take b = 1/2, then a = √3*(1/2) = √3/2. Therefore, vector AF is (0, √3/2, 1/2). Therefore, point F has coordinates A + AF = (0,0,0) + (0, √3/2, 1/2) = (0, √3/2, 1/2).Wait, but in the square ABEF, AF and AB should be adjacent sides. So, point F is connected to A and E, and point E is connected to B and F. Wait, actually, in the square ABEF, the order is A-B-E-F-A. Wait, but AB is the common side, so after AB, the next vertex is E, then F, then back to A? Hmm, maybe I need to check.Alternatively, perhaps the square is A-B-F-E-A. Wait, depends on the orientation. Given that AF is a vector perpendicular to AB, and given the normal vector, perhaps the square is A-B-F-E-A. Let me confirm.If point F is at (0, √3/2, 1/2), then vector BF would be F - B = (0 - 1, √3/2 - 0, 1/2 - 0) = (-1, √3/2, 1/2). The length of BF should be √[(-1)^2 + (√3/2)^2 + (1/2)^2] = √[1 + 3/4 + 1/4] = √[2] which is correct since it's the diagonal of the square. Wait, but BF should be a side of the square, not the diagonal. Wait, no: in square ABEF, the sides are AB, BE, EF, and FA. Wait, confusion arises here.Wait, in square ABEF, the sides should be AB, BE, EF, and FA, but if AB is from A(0,0,0) to B(1,0,0), then BE should be from B(1,0,0) to E, then EF to F, then FA back to A. But if AF is a side, then F is adjacent to A and E. Wait, perhaps I need to reorient.Alternatively, maybe the square is A-F-E-B-A. If AF is a side, then F is connected to A and E, and E is connected to F and B. So, point E would be at B + vector BE, which should be equal to F + vector FE. Hmm, this is getting confusing. Let me approach this step by step.We have points A(0,0,0) and B(1,0,0). We need to find points F and E such that ABEF is a square with sides of length 1, and the plane of ABEF has a normal vector (0, -0.5, √3/2). We have determined point F as (0, √3/2, 1/2). Now, we need to find point E.Since ABEF is a square, vector BE should be equal to vector AF. Vector AF is (0, √3/2, 1/2). Therefore, vector BE should be the same. So starting from B(1,0,0), adding vector BE (0, √3/2, 1/2) gives E(1, √3/2, 1/2). Then, vector EF should be equal to vector AB, which is (-1,0,0). So from E(1, √3/2, 1/2), subtracting 1 in the x-direction gives F(0, √3/2, 1/2), which matches our previous result. Then, vector FA is from F to A, which is (0 - 0, 0 - √3/2, 0 - 1/2) = (0, -√3/2, -1/2), which has length √[(0)^2 + (√3/2)^2 + (1/2)^2] = √[0 + 3/4 + 1/4] = √1 = 1. Good. So the square ABEF has vertices A(0,0,0), B(1,0,0), E(1, √3/2, 1/2), F(0, √3/2, 1/2).Wait, but checking the vectors: AB is (1,0,0), BE is (0, √3/2, 1/2), EF is (-1,0,0), and FA is (0, -√3/2, -1/2). All have length 1, and adjacent sides are perpendicular. Let's check the dot product between AB and BE. AB is (1,0,0), BE is (0, √3/2, 1/2). Their dot product is 1*0 + 0*(√3/2) + 0*(1/2) = 0, so they are perpendicular. Similarly, BE and EF: (0, √3/2, 1/2) · (-1,0,0) = 0*(-1) + (√3/2)*0 + (1/2)*0 = 0. Perpendicular. EF and FA: (-1,0,0) · (0, -√3/2, -1/2) = 0 + 0 + 0 = 0. Perpendicular. FA and AB: (0, -√3/2, -1/2) · (1,0,0) = 0 + 0 + 0 = 0. All adjacent sides are perpendicular, so this is indeed a square. Good.Now, diagonals AC and BF. Diagonal AC in square ABCD is from A(0,0,0) to C(1,1,0). Diagonal BF in square ABEF is from B(1,0,0) to F(0, √3/2, 1/2). So, points M and N are moving along these diagonals with AM = FN.Let me parameterize points M and N. Let’s denote the parameter as t, such that AM = t. Then, since AC has length √2, the coordinates of M can be found by moving t units from A along AC. Similarly, FN = t, so since BF is a diagonal of length √2, moving t units from F towards B would give N. Wait, but FN is the distance from F to N, so if FN = t, then N is located t units away from F along BF.But first, let's confirm the length of BF. Point B is (1,0,0), point F is (0, √3/2, 1/2). The distance BF is √[(1-0)^2 + (0 - √3/2)^2 + (0 - 1/2)^2] = √[1 + 3/4 + 1/4] = √[2] which is correct, as the diagonal of the square.Therefore, diagonal BF has length √2, so if FN = t, then N divides BF such that FN = t and NB = √2 - t. Similarly, AM = t, so M divides AC such that AM = t and MC = √2 - t.To find coordinates of M and N in terms of t, we can parametrize their positions.For point M on AC:AC goes from A(0,0,0) to C(1,1,0). The parametric equation of AC is (t/√2, t/√2, 0) for t from 0 to √2. Wait, but if we use AM = t, then the coordinates of M would be (t/√2, t/√2, 0). Because the vector AC is (1,1,0), which has length √2. So moving t units along AC from A would scale the vector by t/√2, hence coordinates (t/√2, t/√2, 0).Similarly, for point N on BF. BF goes from B(1,0,0) to F(0, √3/2, 1/2). The vector BF is (-1, √3/2, 1/2). The length of BF is √[(-1)^2 + (√3/2)^2 + (1/2)^2] = √[1 + 3/4 + 1/4] = √2, which matches. Since FN = t, moving t units from F towards B. So, starting at F(0, √3/2, 1/2), moving along BF (which is vector (1, -√3/2, -1/2)) for a distance t.The parametric equation for BF can be written as F + s*(vector FB). Vector FB is B - F = (1 - 0, 0 - √3/2, 0 - 1/2) = (1, -√3/2, -1/2). The length of FB is √2. So, parameter s ranges from 0 to √2, with s = 0 at F and s = √2 at B. Therefore, if FN = t, then s = t, because moving t units from F towards B. Therefore, the coordinates of N would be F + (t/√2)*vector FB.Wait, but vector FB has length √2. So, to move t units along BF from F, we need to scale the unit vector in the direction of FB by t. The unit vector in the direction of FB is (1/√2, -√3/(2√2), -1/(2√2)). Therefore, moving t units from F gives N = F + t*(1/√2, -√3/(2√2), -1/(2√2)).But let's compute this step by step. Coordinates of F: (0, √3/2, 1/2). Vector FB: (1, -√3/2, -1/2). To move t units from F towards B, which is along FB. Since the length of FB is √2, the parameterization would be:N = F + (t / √2) * FBSo,N_x = 0 + (t / √2) * 1 = t / √2N_y = √3/2 + (t / √2) * (-√3/2) = √3/2 - (t √3) / (2√2)N_z = 1/2 + (t / √2) * (-1/2) = 1/2 - t / (2√2)Therefore, coordinates of N are (t/√2, √3/2 - (t√3)/(2√2), 1/2 - t/(2√2))Similarly, coordinates of M are (t/√2, t/√2, 0)Now, we need to compute the distance MN as a function of t and then find its maximum.So, coordinates:M = (t/√2, t/√2, 0)N = (t/√2, √3/2 - (t√3)/(2√2), 1/2 - t/(2√2))Therefore, the vector MN is N - M = (t/√2 - t/√2, [√3/2 - (t√3)/(2√2) - t/√2], [1/2 - t/(2√2) - 0])Simplify each component:x-component: 0y-component: √3/2 - (t√3)/(2√2) - t/√2z-component: 1/2 - t/(2√2)So, MN vector is (0, √3/2 - t(√3 + 2)/(2√2), 1/2 - t/(2√2))Wait, let's compute the y-component:√3/2 - (t√3)/(2√2) - t/√2 = √3/2 - t/(2√2)(√3 + 2)Wait, because:(√3)/(2√2) + 1/√2 = (√3 + 2)/2√2 ?Wait, no. Let me factor out t/(2√2):= √3/2 - t/(2√2)(√3 + 2)Yes, because:(√3)/(2√2) + 1/√2 = (√3 + 2)/2√2Therefore, the y-component is √3/2 - t(√3 + 2)/(2√2)Similarly, the z-component is 1/2 - t/(2√2)Therefore, the vector MN is (0, √3/2 - t(√3 + 2)/(2√2), 1/2 - t/(2√2))Now, the distance MN is the magnitude of this vector. Since the x-component is 0, it's just sqrt[(y-component)^2 + (z-component)^2]Let me compute this:MN^2 = [√3/2 - t(√3 + 2)/(2√2)]^2 + [1/2 - t/(2√2)]^2Let me denote s = t/(2√2) to simplify the expression.Then,MN^2 = [√3/2 - s(√3 + 2)]^2 + [1/2 - s]^2Expanding both terms:First term:[√3/2 - s(√3 + 2)]^2 = (√3/2)^2 - 2*(√3/2)*s(√3 + 2) + [s(√3 + 2)]^2= 3/4 - s√3(√3 + 2) + s²(√3 + 2)^2Second term:[1/2 - s]^2 = (1/2)^2 - 2*(1/2)*s + s² = 1/4 - s + s²Adding both terms:MN^2 = 3/4 - s√3(√3 + 2) + s²(√3 + 2)^2 + 1/4 - s + s²Combine constants: 3/4 + 1/4 = 1Combine linear terms: -s√3(√3 + 2) - s = -s[√3(√3 + 2) + 1]Combine quadratic terms: s²(√3 + 2)^2 + s² = s²[(√3 + 2)^2 + 1]Compute √3(√3 + 2) + 1:√3*√3 = 3, so 3 + 2√3 + 1 = 4 + 2√3Compute (√3 + 2)^2 + 1:(3 + 4√3 + 4) + 1 = 8 + 4√3Therefore,MN^2 = 1 - s(4 + 2√3) + s²(8 + 4√3)But s = t/(2√2), so substituting back:MN^2 = 1 - (t/(2√2))(4 + 2√3) + (t^2/(4*2))(8 + 4√3)Simplify:First term: 1Second term: - t/(2√2) * 2*(2 + √3) = - t/(√2)*(2 + √3)Third term: t²/(8)*(8 + 4√3) = t²/(8)*4*(2 + √3) = t²/2*(2 + √3)Therefore,MN^2 = 1 - t(2 + √3)/√2 + t²(2 + √3)/2Let me factor out (2 + √3)/2:MN^2 = (2 + √3)/2 * t² - (2 + √3)/√2 * t + 1Hmm, perhaps this is a quadratic in t. Let me denote k = (2 + √3). Then,MN^2 = (k/2) t² - (k / √2) t + 1This is a quadratic function in t: at² + bt + c, where a = k/2, b = -k/√2, c = 1.The maximum or minimum of MN^2 occurs at t = -b/(2a) = (k/√2)/(2*(k/2)) )= (k/√2)/k = 1/√2Since a = k/2 is positive (k = 2 + √3 > 0), the parabola opens upwards, so the vertex is a minimum. But wait, we are looking for the maximum MN. However, since MN^2 is a quadratic opening upwards, it doesn't have a maximum; it tends to infinity as t approaches ±∞. But in our case, t is constrained between 0 and √2, because AM ranges from 0 to √2 (the length of diagonal AC). Therefore, the maximum of MN must occur at one of the endpoints, either t = 0 or t = √2.Wait, but this contradicts the initial thought. Let me check.Wait, the quadratic MN^2 has a minimum at t = 1/√2, but since the coefficient of t² is positive, the maximum on the interval [0, √2] would be at one of the endpoints. Let's compute MN at t = 0 and t = √2.At t = 0:MN^2 = 1 - 0 + 0 = 1 ⇒ MN = 1At t = √2:MN^2 = (2 + √3)/2 * (√2)^2 - (2 + √3)/√2 * √2 + 1Calculate:First term: (2 + √3)/2 * 2 = (2 + √3)Second term: -(2 + √3)/√2 * √2 = -(2 + √3)Third term: 1Therefore, MN^2 = (2 + √3) - (2 + √3) + 1 = 0 + 1 = 1 ⇒ MN = 1So at both ends t = 0 and t = √2, MN = 1. But that's strange; the minimum occurs at t = 1/√2, so MN would be minimized there, and the maximum is at the endpoints. But this suggests that the maximum MN is 1. However, this seems counterintuitive. Maybe I made an error in the parametrization or calculations.Wait, let me verify with specific points.At t = 0: M is at A(0,0,0), N is at F(0, √3/2, 1/2). The distance AF is 1, as expected. So MN = AF = 1.At t = √2: M is at C(1,1,0), N is at B(1,0,0). The distance CB is √[(1-1)^2 + (1-0)^2 + (0-0)^2] = √[0 + 1 + 0] = 1. So MN = CB = 1.But in between, maybe MN is shorter? So the minimum is somewhere in the middle. But the problem asks for the maximum MN. If both endpoints give MN = 1, and it's a quadratic that opens upwards with minimum at t = 1/√2, then the maximum MN is indeed 1.But wait, the problem states "find the maximum value of MN". If my calculations are correct, then the maximum is 1. But this seems too straightforward. Let me check with t = 1/√2, the midpoint.Wait, t is AM = FN. At t = 1/√2, which is halfway along the diagonals?Wait, AC is length √2, so t ranges from 0 to √2. At t = 1/√2, M is 1/√2 along AC from A, so coordinates ( (1/√2)/√2, (1/√2)/√2, 0 ) = (1/2, 1/2, 0). Similarly, N is 1/√2 along BF from F. Wait, BF is from F(0, √3/2, 1/2) to B(1,0,0). So moving 1/√2 along BF (which is length √2) would reach the midpoint. Therefore, coordinates of N would be the midpoint of BF: (0.5, √3/4, 1/4).Therefore, MN is between (0.5, 0.5, 0) and (0.5, √3/4, 1/4). The distance is sqrt[(0.5 - 0.5)^2 + (0.5 - √3/4)^2 + (0 - 1/4)^2] = sqrt[0 + (0.5 - √3/4)^2 + (1/4)^2].Calculate:0.5 = 2/4, so 2/4 - √3/4 = (2 - √3)/4Thus, ( (2 - √3)/4 )^2 + (1/4)^2 = [ (4 - 4√3 + 3) + 1 ] / 16 = (8 - 4√3)/16 = (2 - √3)/4Therefore, MN = sqrt( (2 - √3)/4 ) = sqrt(2 - √3)/2Numerically, sqrt(2 - √3) ≈ sqrt(2 - 1.732) ≈ sqrt(0.268) ≈ 0.517, so MN ≈ 0.517/2 ≈ 0.258, which is less than 1. So indeed, at t = 1/√2, MN is minimized. Therefore, the maximum MN is indeed 1.But wait, the problem says "the maximum value of MN". If MN is always 1 at the endpoints and less in between, then the maximum is 1. But this seems contradictory to the problem's implication that it's a non-trivial maximum. Maybe there's a mistake in the parametrization.Wait, let's cross-verify with another point. For example, take t = √2 / 2, which is halfway in terms of parameter t.At t = √2 / 2:Coordinates of M: ( (√2/2)/√2, (√2/2)/√2, 0 ) = (1/2, 1/2, 0)Coordinates of N: ( (√2/2)/√2, √3/2 - (√2/2 * √3)/(2√2), 1/2 - (√2/2)/(2√2) )Compute:N_x = ( (√2/2)/√2 ) = (1/2)N_y = √3/2 - ( (√2/2 * √3 ) / (2√2 ) ) = √3/2 - ( (√6 / 2 ) / (2√2 ) ) = √3/2 - ( √6 / (4√2 ) )Simplify √6 / (4√2 ) = (√3 * √2) / (4√2 ) = √3 / 4Thus, N_y = √3/2 - √3/4 = √3/4N_z = 1/2 - ( √2/2 ) / (2√2 ) = 1/2 - (1/4) = 1/4So N is (0.5, √3/4, 1/4), same as before. Wait, that's the same point as when t = 1/√2. But t = √2 / 2 is equal to 1/√2. So yes, that's the same point. So my previous calculation is correct.Thus, MN reaches minimum at t = 1/√2 and maximum at the endpoints t = 0 and t = √2, both giving MN = 1. Therefore, the maximum MN is 1.But the problem states "the planes of squares ABCD and ABEF form a 120° angle". If the maximum distance MN is 1, which is the same as the side length, but since the squares are at an angle, perhaps the maximum distance could be larger? Maybe there's a miscalculation here.Wait, let's consider another approach. Maybe using vectors and dot product to find the distance.Alternatively, consider that MN is the distance between a point on AC and a point on BF, with AM = FN. Maybe the maximum distance occurs when the points are as far apart as possible in 3D space. Since the squares are at 120 degrees, the maximum distance might involve some trigonometric relation.Alternatively, consider that when M and N are at certain positions, their separation in 3D accounts for the angle between the planes. Maybe when M is at A and N is at F, which are in different planes, the distance is 1, but when M is at C and N is at B, the distance is also 1. But perhaps there's another position where MN is longer.Wait, but according to the calculation, MN is always ≤1. Wait, perhaps I made a mistake in the parameterization.Wait, let's check the coordinates again.Point M is on AC: from A(0,0,0) to C(1,1,0). So if AM = t, then since AC is length √2, t ranges from 0 to √2. So coordinates of M are (t/√2, t/√2, 0).Point N is on BF: from B(1,0,0) to F(0, √3/2, 1/2). If FN = t, then since BF is length √2, then N is located t units away from F towards B. So starting at F(0, √3/2, 1/2), moving along BF for t units. The coordinates of N would be:N = F + (t / √2)* vector FBVector FB is (1, -√3/2, -1/2). As BF is of length √2, the unit vector in direction FB is (1/√2, -√3/(2√2), -1/(2√2)).Therefore, moving t units along BF from F:N = (0, √3/2, 1/2) + t*(1/√2, -√3/(2√2), -1/(2√2))So,N_x = 0 + t/√2N_y = √3/2 - t*(√3)/(2√2)N_z = 1/2 - t/(2√2)Which is the same as earlier.Then, coordinates of M are (t/√2, t/√2, 0)Therefore, vector MN is (N_x - M_x, N_y - M_y, N_z - M_z) = (t/√2 - t/√2, [√3/2 - t√3/(2√2) - t/√2], [1/2 - t/(2√2) - 0])Simplify:x-component: 0y-component: √3/2 - t(√3 + 2)/(2√2)z-component: 1/2 - t/(2√2)Then, distance MN is sqrt[(√3/2 - t(√3 + 2)/(2√2))^2 + (1/2 - t/(2√2))^2]This expression simplifies to a quadratic in t, which we found earlier to have a minimum at t = 1/√2 and endpoints at t = 0 and t = √2 both giving MN = 1. Therefore, unless there's a calculation error, the maximum MN is indeed 1.But let's cross-verify with another value, say t = √2/4.At t = √2/4:Coordinates of M: ( (√2/4)/√2, (√2/4)/√2, 0 ) = (1/4, 1/4, 0 )Coordinates of N:N_x = √2/4 / √2 = 1/4N_y = √3/2 - (√2/4)*√3/(2√2) = √3/2 - (√3)/8 = (4√3 - √3)/8 = 3√3/8N_z = 1/2 - (√2/4)/(2√2) = 1/2 - 1/8 = 3/8Therefore, MN is sqrt[(1/4 - 1/4)^2 + (3√3/8 - 1/4)^2 + (3/8 - 0)^2] = sqrt[0 + (3√3/8 - 2/8)^2 + (3/8)^2]Calculate:3√3/8 - 2/8 = (3√3 - 2)/8Thus,MN^2 = [(3√3 - 2)/8]^2 + (3/8)^2Expand:= [ (27 - 12√3 + 4) / 64 ] + 9/64= (31 - 12√3)/64 + 9/64= (40 - 12√3)/64= (10 - 3√3)/16Approximately:√3 ≈ 1.732, so 3√3 ≈ 5.19610 - 5.196 ≈ 4.8044.804 / 16 ≈ 0.3Then sqrt(0.3) ≈ 0.547, which is still less than 1. So MN is indeed smaller than 1 here.Alternatively, pick t = 0. Let me check t = 0:M is at A(0,0,0), N is at F(0, √3/2, 1/2). Distance AF is sqrt[(0)^2 + (√3/2)^2 + (1/2)^2] = sqrt[ 3/4 + 1/4 ] = sqrt[1] = 1.Similarly, t = √2:M is at C(1,1,0), N is at B(1,0,0). Distance CB is sqrt[(1-1)^2 + (1-0)^2 + (0-0)^2] = 1.Thus, the maximum MN is indeed 1. However, this seems counterintuitive because when two squares are at an angle, one might expect points in different planes to have a greater maximum distance. But perhaps due to the constraints AM = FN, the maximum distance is capped at 1.Alternatively, perhaps there's an error in assuming the coordinates. Let me verify the normal vector and the coordinates of point F again.We found the normal vector of ABEF to be (0, -0.5, √3/2), and point F at (0, √3/2, 1/2). Let's confirm if this is correct.Given that the normal vector is (0, -0.5, √3/2), the plane equation is -0.5y + (√3/2)z = 0. Point F is (0, √3/2, 1/2). Plugging into the plane equation:-0.5*(√3/2) + (√3/2)*(1/2) = -√3/4 + √3/4 = 0. Correct.Vector AF is from A(0,0,0) to F(0, √3/2, 1/2), which has length sqrt[0 + (√3/2)^2 + (1/2)^2] = sqrt[ 3/4 + 1/4 ] = 1. Correct.Vector AB is (1,0,0). Vector AF is (0, √3/2, 1/2). Their dot product is 1*0 + 0*(√3/2) + 0*(1/2) = 0, so they are perpendicular. Correct.Thus, the coordinates seem correct. Therefore, the calculations for MN are accurate, leading to MN's maximum value of 1.But let's think differently. Perhaps using the law of cosines for vectors in 3D. The distance MN can be found using the coordinates, but maybe there's a way to express it in terms of the angle between the planes.The angle between the planes is 120 degrees. When you have two points in different planes, the distance between them can be affected by the dihedral angle. However, since AM = FN, the positions of M and N are related.Wait, another approach: since AM = FN, let's denote AM = FN = t. Then, since AC and BF are both length √2, then CM = √2 - t and BN = √2 - t.Coordinates of M: parameter t from A along AC: M = A + (t/√2)(1,1,0) = (t/√2, t/√2, 0)Coordinates of N: since FN = t, starting from F and moving t units towards B along BF. BF vector is B - F = (1, -√3/2, -1/2). Unit vector in BF direction is (1, -√3/2, -1/2)/√[1 + 3/4 + 1/4] = (1, -√3/2, -1/2)/√2.Therefore, N = F + t*(1, -√3/2, -1/2)/√2 = (0, √3/2, 1/2) + t/√2*(1, -√3/2, -1/2)So,N_x = 0 + t/√2*1 = t/√2N_y = √3/2 + t/√2*(-√3/2) = √3/2 - (t√3)/(2√2)N_z = 1/2 + t/√2*(-1/2) = 1/2 - t/(2√2)Which matches earlier coordinates. Therefore, the expression for MN is correct.Then, MN^2 = [√3/2 - t(√3 + 2)/(2√2)]^2 + [1/2 - t/(2√2)]^2Expanding this:First term:= ( (√3/2)^2 ) - 2*(√3/2)*(t(√3 + 2)/(2√2)) + ( t(√3 + 2)/(2√2) )^2= 3/4 - ( t√3(√3 + 2) )/(2√2) + ( t²(√3 + 2)^2 )/(8 )Second term:= (1/2)^2 - 2*(1/2)*(t/(2√2)) + ( t/(2√2) )^2= 1/4 - t/(2√2) + t²/(8 )Adding both terms:MN^2 = 3/4 + 1/4 - ( t√3(√3 + 2) )/(2√2) - t/(2√2) + ( t²(√3 + 2)^2 )/(8 ) + t²/(8 )Simplify:= 1 - t/(2√2)(√3(√3 + 2) + 1 ) + t²/(8 )( (√3 + 2)^2 + 1 )Compute coefficients:√3(√3 + 2) + 1 = 3 + 2√3 + 1 = 4 + 2√3(√3 + 2)^2 + 1 = 3 + 4√3 + 4 + 1 = 8 + 4√3Thus,MN^2 = 1 - t(4 + 2√3)/(2√2) + t²(8 + 4√3)/8Simplify coefficients:= 1 - t(2 + √3)/√2 + t²(2 + √3)/2Which is the same quadratic in t as before. So, the maximum occurs at the endpoints t = 0 and t = √2, giving MN = 1.Therefore, after thorough calculation and verification, the maximum value of MN is 1. But this seems underwhelming. Is there something missing here?Wait, maybe I misinterpreted the problem. Let me re-read the problem statement."Planes of squares ABCD and ABEF form a 120° angle. Points M and N are on diagonals AC and BF respectively, and AM = FN. If AB = 1, find the maximum value of MN."No, the problem seems correctly interpreted. Squares share side AB, planes at 120 degrees, points M and N on diagonals with AM = FN, find max MN.But according to calculations, the maximum MN is 1. But AB is length 1, and MN reaches up to 1. Maybe that's correct. For example, when M is at A and N is at F, which are in different planes, the distance is 1, which is the length of AF. Similarly, when M is at C and N is at B, the distance is CB = 1.Therefore, the maximum MN is indeed 1. However, since the problem is presented as requiring a systematic thinking process, and the answer seems straightforward, I must ensure there's no oversight.Another way to think about it: since AM = FN, and diagonals AC and BF are both length √2, perhaps there's a symmetry that when M and N are at corresponding points, their distance is constrained. However, given the dihedral angle, one might expect that the maximum distance occurs when M and N are as far apart as possible in 3D space. However, due to the condition AM = FN, their movement is synchronized, limiting the maximum possible distance.Alternatively, consider that when M moves from A to C, N moves from F to B. The points A and F are separated by 1 unit, and C and B are separated by 1 unit. The path of M and N are such that their distance doesn't exceed 1. Hence, the maximum MN is 1.Therefore, after careful analysis, the maximum value of MN is indeed 1.Final Answerboxed{1}

✅:Given two squares (ABCD) and (ABEF) sharing the side (AB) and forming a dihedral angle of (120^circ), we need to find the maximum value of (MN) where points (M) and (N) are on diagonals (AC) and (BF) respectively, such that (AM = FN). The side length (AB = 1).1. Coordinate System Setup: - Place (A) at the origin ((0,0,0)) and (B) at ((1,0,0)). - Square (ABCD) lies in the (xy)-plane with (C(1,1,0)) and (D(0,1,0)). - Square (ABEF) forms a (120^circ) dihedral angle with (ABCD). The normal vector of (ABEF) is determined to be ((0, -0.5, sqrt{3}/2)) after considering the rotation around (AB).2. Coordinates of Points in (ABEF): - Point (F) is determined to be ((0, sqrt{3}/2, 1/2)). - Diagonal (BF) in (ABEF) has coordinates from (B(1,0,0)) to (F(0, sqrt{3}/2, 1/2)).3. Parameterization of Points (M) and (N): - For (M) on (AC), parameterize (AM = t) giving (M(t/sqrt{2}, t/sqrt{2}, 0)). - For (N) on (BF), parameterize (FN = t) giving (N(t/sqrt{2}, sqrt{3}/2 - tsqrt{3}/(2sqrt{2}), 1/2 - t/(2sqrt{2}))).4. Distance Calculation: - Vector (MN) is calculated as ((0, sqrt{3}/2 - t(sqrt{3} + 2)/(2sqrt{2}), 1/2 - t/(2sqrt{2}))). - The magnitude of (MN) is derived as a quadratic function in (t), showing that the maximum value occurs at the endpoints (t = 0) or (t = sqrt{2}).5. Verification: - At (t = 0), (M = A) and (N = F), giving (MN = 1). - At (t = sqrt{2}), (M = C) and (N = B), giving (MN = 1).Thus, the maximum value of (MN) is (boxed{1}).

🔑:1. Construct Geometrical Relationships: - Consider the squares ABCD and ABEF sharing the common side AB. - The angle formed between the planes ABCD and ABEF is 120^circ. - Points M and N are located on the diagonals AC of ABCD and BF of ABEF, respectively, such that AM = FN and AB = 1.2. Introduce Perpendiculars and Angles: - Draw MP perp AB at point P and connect PN. It can be shown that PN perp AB because AC perp AB and BF perp AB. - Thus, angle MPN = 120^circ.3. Setup Variables and Calculate Lengths: - Let AM = FN = x. - Given that AB = 1 and using the property of a square with unit side length, the diagonal of square ABCD has length sqrt{2}. - Therefore, AP = MP = frac{x}{sqrt{2}} and PN = frac{sqrt{2} - x}{sqrt{2}}.4. Apply Cosine Rule: - In triangle MPN, use the Law of Cosines to find MN: [ MN^2 = MP^2 + PN^2 - 2 cdot MP cdot PN cos(120^circ). ] Given cos(120^circ) = -frac{1}{2}: [ MN^2 = left(frac{x}{sqrt{2}}right)^2 + left(frac{sqrt{2} - x}{sqrt{2}}right)^2 - 2 cdot left(frac{x}{sqrt{2}}right) cdot left(frac{sqrt{2} - x}{sqrt{2}}right) cdot left(-frac{1}{2}right). ]5. Simplify the Expression: - Compute MN^2 step by step: [ MN^2 = frac{x^2}{2} + frac{(sqrt{2} - x)^2}{2} + frac{x(sqrt{2} - x)}{2}. ] Simplify further: [ MN^2 = frac{x^2}{2} + frac{2 - 2sqrt{2}x + x^2}{2} + frac{xsqrt{2} - x^2}{2}. ] [ MN^2 = frac{x^2}{2} + frac{2 - 2sqrt{2}x + x^2}{2} + frac{xsqrt{2}}{2} - frac{x^2}{2}. ] Combine like terms: [ MN^2 = frac{x^2 + 2 - 2sqrt{2}x + x^2 + xsqrt{2} - x^2}{2}. ] [ MN^2 = frac{2x^2 + 2 - sqrt{2}x}{2}. ]6. Further Simplification and Maximization: - Collect terms to ease finding maximum: [ MN^2 = frac{2 + x^2 - sqrt{2}x}{2}. ] Observe: [ MN^2 = frac{2}{2} + frac{x^2}{2} - frac{sqrt{2}x}{2} = 1 + frac{x^2}{2} - frac{sqrt{2}x}{2}. ]7. Evaluate the Maximum Value: - Recognize the quadratic form and set up for critical points: [ MN = sqrt{1 + frac{x^2}{2} - frac{sqrt{2}x}{2}}. ] - Case values: - For x = 0: MN^2 = 1. - For x = sqrt{2}: MN^2 = 1.Conclusion:The maximum value of MN occurs when ( x = 0 ) or ( x = sqrt{2} ), thus giving ( MN = 1 ).(boxed{1})